Description
「世上没有无价的情报,」玘露出一丝满意的微笑。
「你懂我的意思吧?」
寒收回手。
玘给出了他留给寒的题。
既然紫堇和彼岸花给予了我们异色的瞳孔,我们理所应当是连接在一起的。我称一棵树上的一个点集是“连接的”,当且仅当树上存在一条链能够覆盖这个点集并且这个集合大小不小于 2。我们是独一无二的,可是你知道,一棵树,总是连起来的啊。
「然后呢?」
「现在,你需要告诉我每个点被多少个这样的点集所包含。」
玘飘然而去。
湖底之城那封存已久的记忆,被彼岸花和紫堇的力量,揭开了封印的一角。
第一行一个正整数 n 表示这棵树有 n 个点编号为 1∼n。
接下来 n−1 行,每行两个正整数 u,v 描述一条边。
为了防止输出量过大,本题采用以下的输出方式。
设 ansi 为包含 i 号节点的连接的集合的个数对 109+7 取模得到的值,你需要输出 xori=1nansi×i 的值。注意这里没有取模运算。
4
1 2
2 3
2 4
18
Hint
样例解释
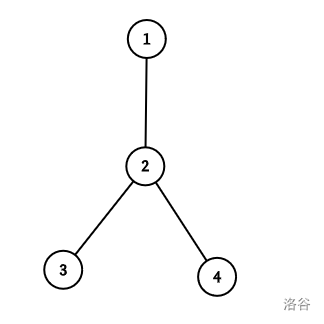
连接的集合有以下一些:
- {1,2}
- {1,3}
- {1,4}
- {2,3}
- {2,4}
- {3,4}
- {1,2,3}
- {1,2,4}
- {2,3,4}
如 {1,3,4} 就不是一个连接的集合,因为你找不出一条链使得 {1,3,4} 为它的子集。
其中 1,2,3,4 号节点分别在 5,6,5,5 个集合中出现。通过计算可得 xori=1nansi×i=18。
数据范围
本题采用捆绑测试。
| 子任务编号 |
数据范围 |
特殊性质 |
分值 |
时间限制 |
| Subtask1 |
n≤20 |
|
15 |
1s |
| Subtask2 |
n≤100 |
| Subtask3 |
n≤3×103 |
20 |
| Subtask4 |
n≤5×105 |
A |
15 |
2s |
| Subtask5 |
|
35 |
特殊性质 A:保证树退化成一条链。
对于 100% 的数据 1≤u,v≤n≤5×105。


 京公网安备 11011102002149号
京公网安备 11011102002149号