Description

悦正在寻找她的记忆。忽然，她来到了有 $n$ 个节点的一棵树上。树上每一条边都有各自边权，每一个点都有各自的点权。

「把经历都聚拢起来，能完整地复原吗……」

悦从树上的一个点，慢慢地走到了另一个点，可是她什么也没找到。但是，她不知道，玘一直在远处望着她走过的道路。

玘发现，悦全程没有走回头路。他想把悦走过的每一条边的边权乘起来，可惜他发现他遇到了一个这一生未曾见到过的数字。

「为什么会这样呢？」

玘想到悦是突然出现在树上的，最初的点一定有蹊跷！他把最初那个点的点权乘上……

突然，一束彼岸花的红光亮起！世界重新安静了下来。

悦看到了玘留下的字样，可惜她不能从中看出任何过去的记忆。现在，你要帮她判断：把经历都聚拢起来，能完整地复原过去吗？我们称悦的一条路径能“复原过去”，当且仅当玘留下的乘积是一个整数。

形式化题面

给定一棵 $n$ 个节点的树和 $q$ 次询问。每次询问给出两个整数 $x,y$，表示询问树上以 $x$ 和 $y$ 为端点的简单路径上边权乘积与点 $x$ 的点权相乘是否为整数。

Input Format

第一行两个正整数 $n$ 和 $q$，表示树上有 $n$ 个节点编号为 $1\sim n$，悦在树上走了 $q$ 条路径。

接下来一行 $n$ 个非负整数表示每个点的点权 $a_i$。

接下来 $n-1$ 行每行两个正整数 $u,v$ 和一个非负实数 $w$ 表示 $u,v$ 间有一条边权为 $w$ 的边。

接下来 $q$ 行，每行两个正整数 $x,y$，表示悦从点 $x$ 开始走到了点 $y$。

Output Format

对于悦的每一次询问，你需要输出一行一个字符串。如果悦能够成功复原她的过去，请输出 Yes，否则请输出 No。

5 3
1 2 3 4 5
1 2 0.1
2 3 0.20
3 4 0.5
2 5 0.99
1 5
1 4
4 3

No
No
Yes

Hint

样例解释

根据输入可以得到下图：

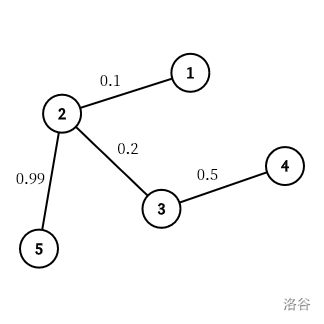
对于第一个询问 $(1,5)$ 可以发现悦经过的边的边权分别是 $0.1$ 和 $0.99$，她出发的 $1$ 号点的点权为 $1$。$1\times0.1\times0.99=0.099$ 不是整数。所以输出 No。

对于后面两次询问同理。

数据范围

本题采用捆绑测试。

特殊性质 $\text{A}$：保证树退化成一条链。

特殊性质 $\text{B}$：保证树随机生成（即对于每一个节点随机选择它的父亲节点）。

特殊性质 $\text{C}$：保证 $w\in\{0.1,0.3,0.5,0.7,0.9\}$。

特殊性质 $\text{D}$：保证 $w\in\{0.1,0.2,0.3,0.4,0.6,0.7,0.8,0.9\}$。

特殊性质 $\text{E}$：保证 $w\le2$ 且 $w$ 小数位数不超过 $1$ 位。

对于 $100\%$ 的数据满足 $1\le n,q\le2\times10^5$，$0\le a_i\le10^9$，$0\le w\le10^4$，$1\le u,v,x,y\le n$，$x\ne y$，$w$ 小数位数不超过 $4$ 位。