Description

学生社会可以被看作一个排列成等腰直角三角形的节点阵列。该节点阵列共有 $n$ 行，第 $i$ 行共有 $i$ 个节点。我们将第 $i$ 行第 $j$ 列的节点，标号为 $(i,j)$。

• 这些节点具有权值。具体而言，节点 $(i,j)$ 的权值为 $r_i\oplus c_j$，其中 $r$ 和 $c$ 是给定的 $01$ 序列，$\oplus$ 是二进制异或操作。
• 这些节点有边相连。具体而言，对于 $1\le i< n$，$1\le j\le i$，会有一条边连接 $(i,j)$ 和 $(i+1,j)$。此外，对于 $2\le i\le n$，还会有边连接 $(i,i)$ 和 $(i-1,a_i)$。其中 $a$ 是给定的序列。

现在你需要从这些节点中，选出一些节点，使得这些节点间两两不存在边相连，最大化选出来的节点的权值之和。

如下图所示，是 $n=8$ 的一个例子。黑色节点权值为 $1$，白色节点权值为 $0$。

注：图片中只象征性地给出了部分 $r_i$ 和 $c_i$ 的值。该图片上实际 $\def\t{,\allowbreak}r=\{1\t 1\t 0\t 1\t 0\t 0\t 0\t 1\}\t c=\{0\t 0\t 1\t 0\t 1\t 1\t 0\t 0\}$。

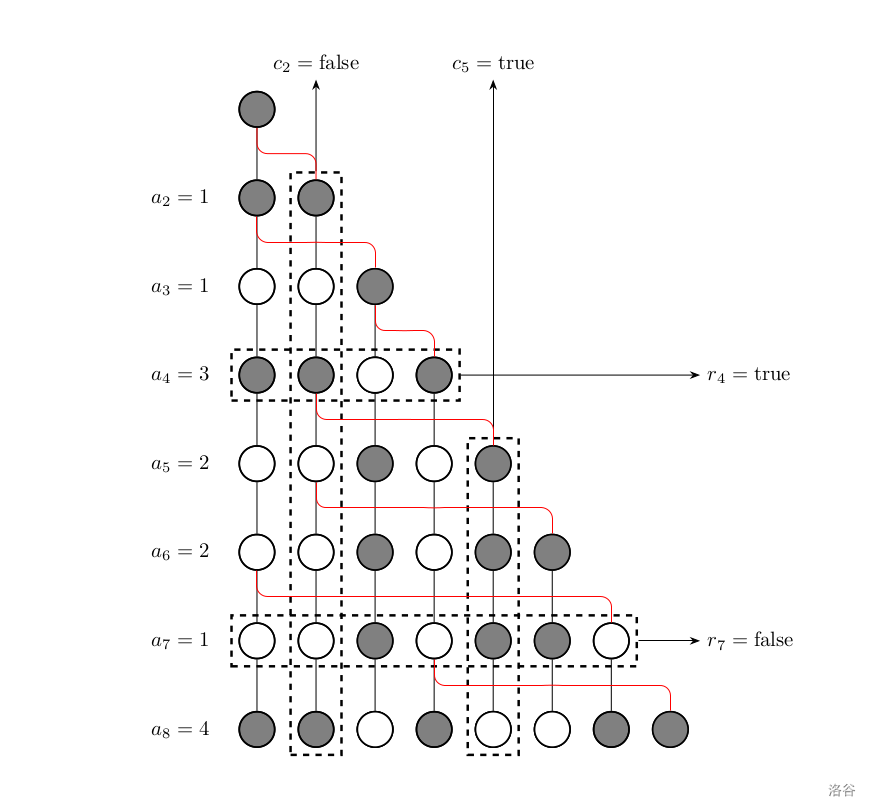
Input Format

• 第一行有一个正整数 $n$，描述节点阵列的大小。
• 第二行有 $n$ 个整数 $0$ 或者 $1$，描述 $r_i$ 的值。
• 第三行有 $n$ 个整数 $0$ 或者 $1$，描述 $c_i$ 的值。
• 第四行有 $n-1$ 个正整数，其中第 $i$ 个数描述 $a_{i+1}$ 的值。

Output Format

• 输出共一行一个整数，描述选出的节点的权值之和的最大值。

8
1 1 0 1 0 0 0 1
0 0 1 0 1 1 0 0
1 1 3 2 2 1 4

14

Hint

样例解释

一种可能的选择方案如下图所示。橘红色方块表示选中的节点。

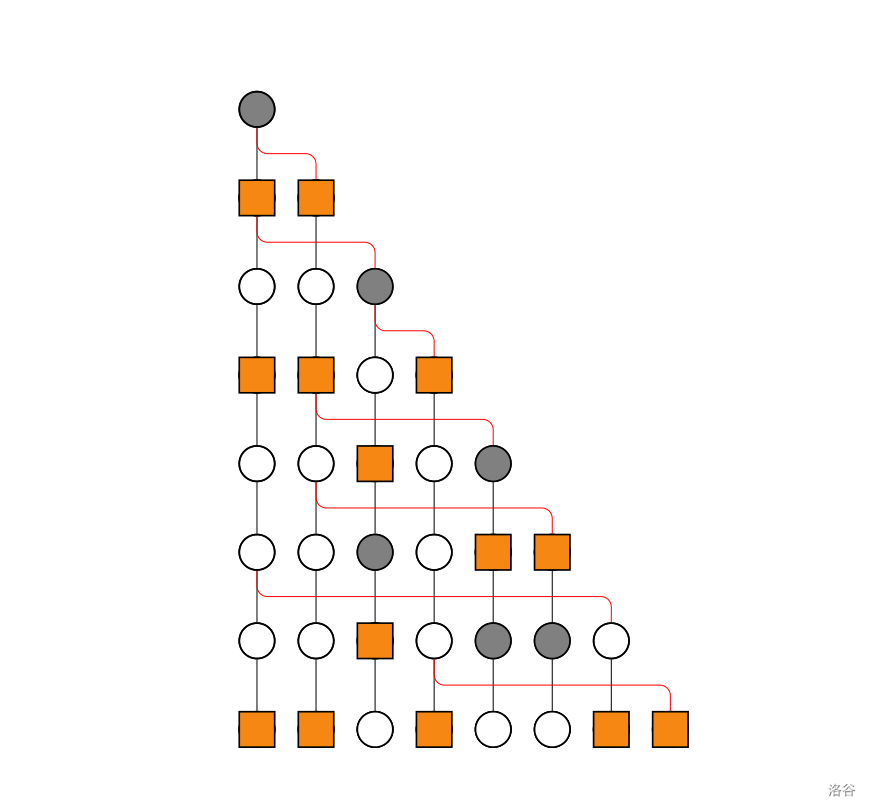
数据范围及约定

对于全部数据，保证 $1\le n\le 10^6$，$r_i\in\{0,1\}$，$c_i\in\{0,1\}$，$1\le a_i<i$。