题目描述

小蓝有大量正方体的积木（所有积木完全相同），他准备用积木搭一个巨大的图形。

小蓝将积木全部平铺在地面上，而不垒起来，以便更稳定。他将积木摆成一行一行的，每行的左边对齐，共 $n$ 行，形成最终的图形。

第一行小蓝摆了 $H_{1}=w$ 块积木。从第二行开始，第 $i$ 行的积木数量 $H_{i}$ 都 至少比上一行多 $L$，至多比上一行多 $R$ (当 $L=0$ 时表示可以和上一行的积木数量相同)，即

给定 $x, y$ 和 $z$, 请问满足以上条件的方案中，有多少种方案满足第 $y$ 行的积木数量恰好为第 $x$ 行的积木数量的 $z$ 倍。

输入格式

输入一行包含 $7$ 个整数 $n, w, L, R, x, y, z$，意义如上所述。

输出格式

输出一个整数，表示满足条件的方案数，答案可能很大，请输出答案除以 $998244353$ 的余数。

5 1 1 2 2 5 3

4

233 5 1 8 100 215 3

308810105

提示

【样例说明】

符合条件的积木如图所示

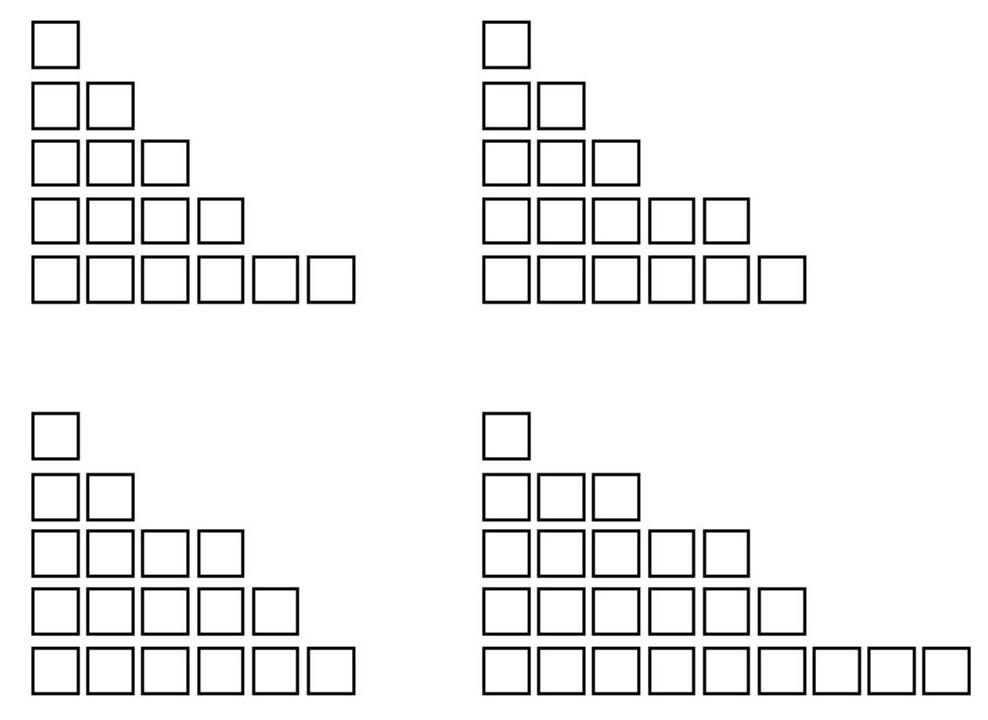
【评测用例规模与约定】

对于 $10 \%$ 的评测用例, $1 \leq n \leq 10,1 \leq w \leq 10,0 \leq L \leq R \leq 3$;

对于 $20 \%$ 的评测用例, $1 \leq n \leq 20,1 \leq w \leq 10,0 \leq L \leq R \leq 4$;

对于 $35 \%$ 的评测用例, $1 \leq n \leq 500,0 \leq L \leq R \leq 10$;

对于 $50 \%$ 的评测用例, $1 \leq n \leq 5000,0 \leq L \leq R \leq 10$;

对于 $60 \%$ 的评测用例, $1 \leq n \leq 20000,0 \leq L \leq R \leq 10$;

对于 $70 \%$ 的评测用例, $1 \leq n \leq 50000,0 \leq L \leq R \leq 10$;

对于 $85 \%$ 的评测用例, $1 \leq n \leq 3\times10^5,0 \leq L \leq R \leq 10$;

对于所有评测用例, $1 \leq n \leq 5\times10^5, 0 \leq w \leq 10^{9}, 0 \leq L \leq R \leq 40$, $1 \leq x<y \leq n, 0 \leq z \leq 10^{9}$ 。

蓝桥杯 2021 国赛 A 组 J 题。