题目描述

诸由杨是一名咸鱼大学生，虽然他每天仍然幻想着在多项式时间内解决 NPC 问题。

诸由杨上课的时候了解到子图同构问题是一个 NPC 问题。他打算给出一个子图同构问题的多项式判定算法，间接地去证明 P = NP，这样他一定可以凭借这个伟大的工作荣获图灵奖！只可惜诸由杨才疏学浅，连子图同构问题属于 NPC 的证明都没有想出来。因而他退而求其次，准备判定一个更加简单的问题：

给定两棵有根树 $G, H$。设 $\lvert G \rvert$ 代表树 $G$ 中的节点个数，则这两棵树满足如下限制：$1 \leq \lvert H \rvert \leq \lvert G \rvert \leq \lvert H \rvert + k$。这里诸由杨保证 $k$ 是一个小常数。

诸由杨可以删除 $G$ 中的若干个节点，假定删除节点后后得到的子图为 $G'$。他想要知道是否存在一种删除节点的方式，使得删除后得到的子图 $G'$ 满足如下条件：

• $G'$ 连通。
• $G'$ 包含 $G$ 中的根节点（也就是说 $G$ 根节点在删除过程中没有被删除）。
• $G'$ 和 $H$ 同构（也就是说存在一种让 $G'$ 中点重标号的方式，使得重标号得到的图和 $H$ 完全相同，且 $G$ 中的根节点经过重标号后恰好为 $H$ 的根节点）。

输入格式

本题有多组测试数据。

输入的第一行依次包含两个正整数 $C,T$ 和一个非负整数 $k$，三个数字分别表示当前测试点编号，测试数据组数和题目中给定的常数。如果当前测试数据为样例则 $C = 0$。保证 $T \leq 500$、$k \leq 5$。

对于每一组测试数据：

输入的第一行包含一个正整数 $n_1$，表示树 $G$ 中的节点个数，保证 $1 \leq n_1 \leq {10}^5$，且 $\sum n_1 \leq 5 \times {10}^5$。

输入的第二行包含 $n_1$ 个整数，描述了树 $G$ 的结构。具体地，第 $i$（$1 \leq i \leq n_1$）个整数 $a_i$ 表示在树 $G$ 中节点 $i$ 的父节点，如果其为根节点则 $a_i = -1$。保证按照上述规则得到的树为连通有根树。

输入的第三行包含一个正整数 $n_2$，表示 $H$ 中的节点个数，保证对于所有测试数据，满足 $\max(1, n_1 - k) \leq n_2 \leq n_1$。

输入的第四行包含 $n_2$ 个整数，描述了树 $H$ 的结构。具体地，第 $i$（$1 \leq i \leq n_2$）个整数 $b_i$ 表示在树 $H$ 中节点 $i$ 的父节点，如果其为根节点则 $b_i = -1$。保证按照上述规则得到的树为连通有根树。

输出格式

对于每一组测试数据：

输出一行一个字符串。如果存在删除 $G$ 中节点的方式，使得其能够同时满足上述三个条件，则输出 Yes；否则输出 No。

0 3 1
3
2 -1 2
2
-1 1
4
3 3 -1 3
3
2 3 -1
5
-1 1 5 5 1
5
2 3 -1 3 2

Yes
No
Yes

提示

【样例解释 #1】

对于第一个测试点，我们删除第一棵树的 $1$ 号节点。此时剩余的树和输入第二棵树均为包含两个节点的有根树，因而输出为 Yes。

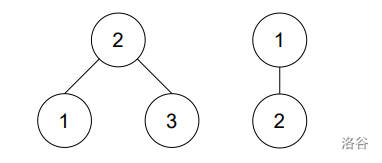
对于第二个测试点，输入第一颗树深度为 $1$，但是输入第二颗树深度为 $2$。因而不论如何删除第一颗树的节点不会导致其树高增加到 $2$，因而输出为 No。

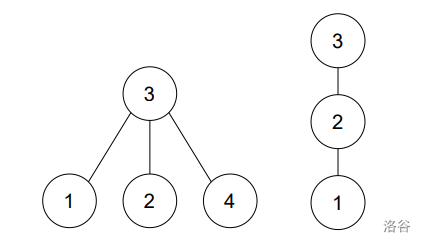
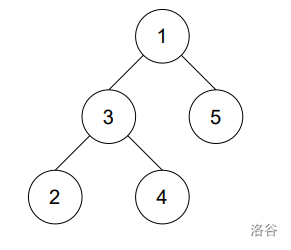
对于第三个测试点，其输入两颗树均同构于下图的树，因而因而输出为 Yes。

---

【样例 #2】

见附件中的 iso/iso2.in 与 iso/iso2.ans。

该样例数据范围满足测试点 $7 \sim 8$。

---

【样例 #3】

见附件中的 iso/iso3.in 与 iso/iso3.ans。

该样例数据范围满足测试点 $9 \sim 10$。

---

【样例 #4】

见附件中的 iso/iso4.in 与 iso/iso4.ans。

该样例数据范围满足测试点 $13$。

---

【数据范围】

对于所有测试数据，满足 $1 \leq T \leq 500$，$1 \le n_2 \leq n_1 \le {10}^5$，$\sum n_1 \leq 5 \times {10}^5$，$0 \leq k \leq 5$。各测试点的附加限制如下表所示：

$n_1,n_2$	$\sum n_1$	测试点	$k$	特殊性质
$\leq 8$	$\leq 500$	$1 \sim 3$	$\leq 0$	无
		$4 \sim 6$	$\leq 5$
$\leq 16$	$\leq 10^3$	$7 \sim 8$	$\leq 0$
		$9 \sim 10$	$\leq 5$
$\leq 150$	$\leq 10^4$	$11$	$\leq 0$
		$12$	$\leq 1$
		$13$	$\leq 5$
$\leq 10^5$	$\leq 5 \times 10^5$	$14 \sim 16$	$\leq 0$	A
		$17 \sim 20$		B
		$21$	$\leq 1$	无
		$22 \sim 23$	$\leq 3$
		$24 \sim 25$	$\leq 5$

其中附加限制中的特殊性质如下所示：

• 特殊性质 A：保证有根树 $G$ 每个节点要么是叶节点，要么有恰好 $1$ 个儿子结点；另一种等价的表述是有根树 $G$ 构成了一条链，且根节点为链的一个端点。
• 特殊性质 B：保证有根树 $G$ 每个节点要么是叶节点，要么有恰好 $2$ 个儿子结点，同时保证 $G$ 的每一个叶节点深度均相同；另一种等价的表述是有根树 $G$ 构成一棵完全二叉树，且根节点为完全二叉树的根节点。

【提示】

数据没有针对任何合理的哈希算法做任何针对性的构造，所以在合理范围内不需要过度担心因为哈希碰撞而产生的失分问题。