题目背景

「人类的梦想之一，月面旅行对一般人也终于成为可能！」
「从下个月起日本各个旅行公司将开始展开旅行」

然而，月球的表面，有着将月之都与荒凉的无生命星球隔开的一道结界。只要这道结界存在，人们只能看到石头罢了。

而月面旅行的费用，也绝不是身为大学生的莲子与梅莉二人所能承担的。但是，她们想要探寻的是，被结界所包裹的，有着高度发达文明的月之都。

这，便是另一侧的月。梅莉她看见了。兔子在捣药，身着华美的服装，优雅地在天空中起舞的天女。

「我说莲子啊。如果月面旅行太贵实在不行的话，我们要不要试着想点别的办法去月球呢？」

题目描述

简要题意

给定 $n$ 个节点的树（保证 $n\ge 2$），Hifuu 和 Luna 交替操作，前者先手。每回合操作者选择一个节点，将「该节点」和「所有与该节点相连的边」删除，形成若干个连通块，操作者再从中保留一个连通块。如果该回合结束后只剩下一个节点，则该回合的操作者失败，另一个人胜利。问谁存在必胜策略。

---

原始题意

但是，月之都是有结界保护的，也就是说莲子与梅莉若是想要用一些方式完成月球旅行，势必要突破这层结界。

月之都的结界是由 $n$ 个节点，$n-1$ 条灵能输送渠道构成的连通的结构，其中节点编号为 $1 \sim n$。结界有一个中枢控制系统，以提防外界的人闯入结界，抵达月之都。莲子和梅莉便需要与这个控制系统进行一些交互，才能进入月之都。

具体而言，莲子梅莉，和中枢控制系统是交替进行操作的，其中莲子梅莉是先手。操作方可以任意选择结界上的一个节点，将连向这个节点的所有灵能输送渠道全部断绝，同时废弃这个节点。这也就意味着，这会把结界分为若干组节点，每一组节点之间没有灵能输送渠道，而组内的节点由灵能输送渠道相连。在这些节点组中，操作者可以任意保留一组节点，将另外所有节点全部废弃，即，之后再也无法操作这些被废弃的节点了。

在这样的规则之下，若操作结束后，最后只剩下一个节点，那么操作者失败，另一个人取得胜利。现在莲子和梅莉希望知道，在这样的规则之下，她们是否存在一种必定能够抵达月之都的策略？

输入格式

本题多组数据。第一行输入一个正整数 $T$，表示数据组数。对于每一组数据：

• 第一行有一个正整数 $n$。
• 接下来 $n-1$ 行，每行两个正整数 $u_i,v_i$。表示一条连接节点 $u_i$ 和 $v_i$ 的双向的灵能输送渠道。

输出格式

对于每一组数据，输出莲子和梅莉是否能够到达月之都。具体而言，若她们存在必定能到达月之都的策略，则输出 $\texttt{Hifuu}$，否则输出 $\texttt{Luna}$。

1
5
2 4
1 2
3 1
5 2

Hifuu

1
11
1 2
1 3
1 4
2 5
2 6
4 7
5 8
5 9
9 10
9 11

Hifuu

1
2
1 2

Luna

提示

样例解释

样例 #1

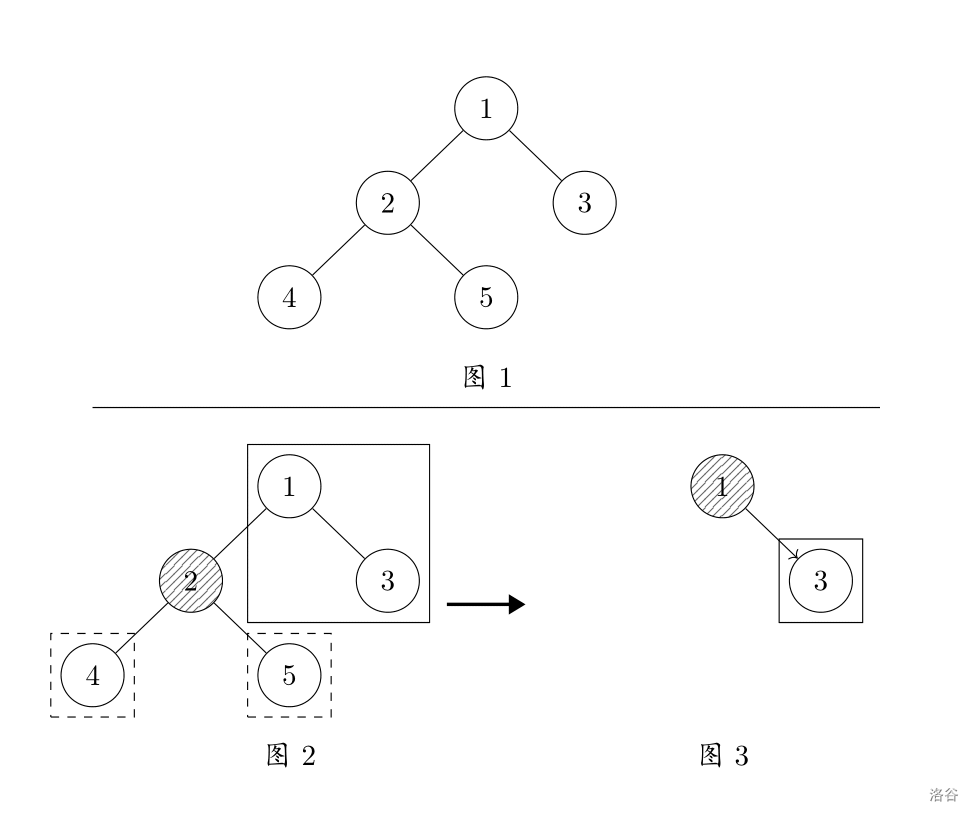
图 $1$ 是结界。图 $2$、图 $3$ 展示了一种莲子和梅莉可能的一种必胜策略：选择节点 $2$，然后保留 $\{1,3\}$ 所处的连通块，那么中枢控制系统无论是选择节点 $1$ 还是 $3$ 都必输。

样例 #2

---

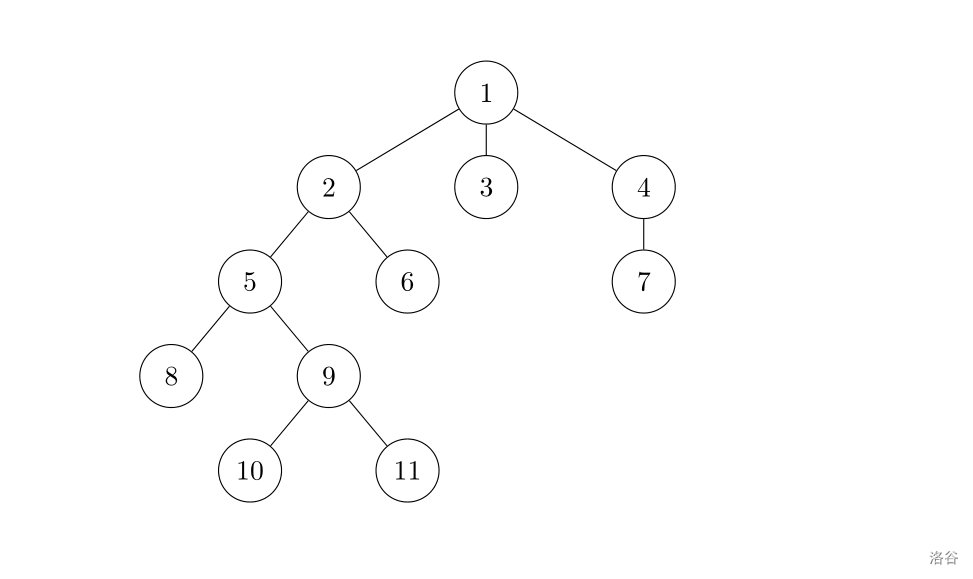
数据范围

本题采用捆绑测试。

$$\def\arraystretch{1.5} \begin{array}{|c|c|c|c|c|}\hline \textbf{Subtask} & \textbf{\textsf{分值}} & \bm{n\le } & \textbf{\textsf{特殊性质}} & \textbf{Subtask \textsf{依赖}}\cr\hline 1 & 15 & 8 & - & - \cr\hline 2 & 20 & 10^5 & \mathbf{A} & -\cr\hline 3 & 20 & 10^5 & \mathbf{B} & - \cr\hline 4 & 15 & 10^3 & - & 1 \cr\hline 5 & 30 & 10^5 & - & 2,3,4 \cr\hline \end{array} $$

• 特殊性质 $\mathbf{A}$：保证存在一个点度数为 $n-1$。
• 特殊性质 $\mathbf{B}$：保证 $n=2^k-1,k \in \N^*$。且树的形态是完全二叉树。

对于 $100\%$ 的数据：$1 \leq T \leq 5$，$2 \le n \le 10^5$，输入数据构成一棵树。