题目描述

你有一张形状为正 $n$ 边形的柱形拼图，它由一个中间块，$n$ 个边缘块和 $n$ 个角块拼成，正 $n$ 边形的每条边上有两个角块和一个边缘块。（如下图即为 $n=5$ 时拼图的俯视图，蓝色为角块，红色为边缘块，灰色为中间块）

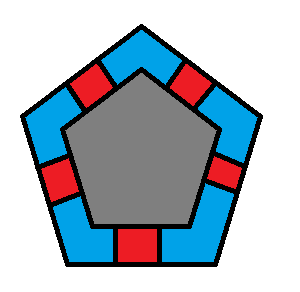
每个边缘块有顶部底部和向外裸露的面总共三个面上是有颜色的，每个面上的颜色不一定相同。而每个角块上向外裸露的面有两个，所以总共四个面上是有颜色的，每个面上的颜色也不一定相同。而中间块只有顶部和底部是有颜色的。

我们将角块与边缘块逆时针标号，正 $n$ 边形的第 $i(i<n)$ 条边的侧面由第 $i$ 块角块的逆时针方向侧面，第 $i$ 块边缘块与第 $i+1$ 块的角块的顺时针方向侧面组成。特别地，第 $n$ 条边的侧面由第 $n$ 块角块的逆时针方向侧面，第 $n$ 块边缘块与第 $1$ 块的角块的顺时针方向侧面组成。

接着，你可以执行如下的操作：选择拼图的一条边并将两边的角块交换后上下反转（注意此时两个侧面会互换）并且边上的边缘块也上下反转。

我们称一个平面是整齐的当且仅当平面上颜色均相同，现在你要通过若干次操作，来使得这个拼图上的每个面都是整齐的。

输入格式

第一行一个正整数 $n$。

接下来两个正整数 $col_{tp},col_{bt}$ 分别表示中间块顶部的颜色和底部的颜色。

接下来 $n$ 行，每行四个整数 $ct_i,cl_i,cr_i,cb_i$ 分别表示第 $i$ 个角块的顶部颜色，逆时针方向侧面颜色，顺时针方向侧面颜色以及底部颜色。

接下来 $n$ 行，每行三个整数 $et_i,es_i,eb_i$ 分别表示第 $i$ 个边缘块的顶部颜色，侧面颜色以及底部颜色。

输出格式

如果无解，输出 $-1$。

否则先输出一行一个整数表示操作次数 $m$，接下来一行 $m$ 个整数表示第 $i$ 操作的边编号。

你需要保证操作次数不超过 $100000$，多解输出任意一种即可。

4
0
5
5 4 3 0
0 1 2 5
0 2 3 5
5 1 4 0
0 1 5
0 2 5
5 3 0
0 4 5

5
1 2 3 2 1

提示

样例解释

如下图

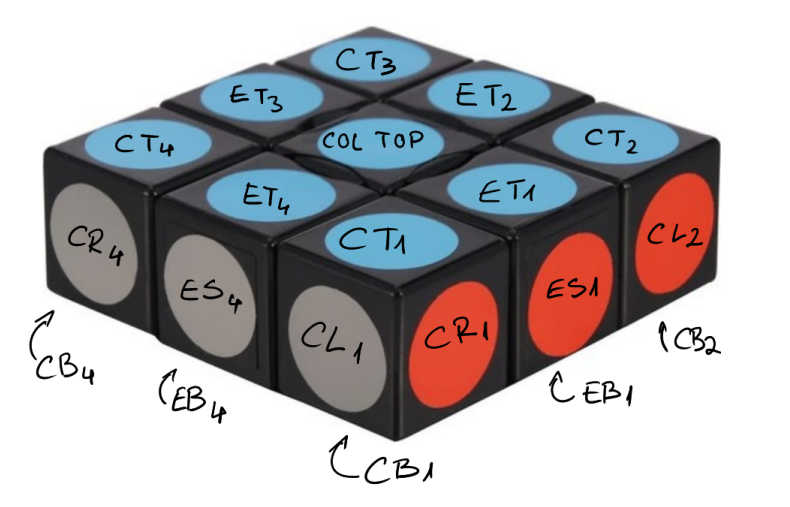
数据规模与约定

对于 $100\%$ 的数据，保证 $4\leq n \leq 100$，$0\leq ct_i,cl_i,cr_i,cb_i\leq n+1$，$\{es_1,es_2,...,es_n,col_{tp},col_{bt}\}$ 构成一个 $0\sim n+1$ 的排列。

说明

翻译自 AGM 2022 Qualification Round F Kube。