#P8117. 「Wdoi-1.5」旅人 1977
「Wdoi-1.5」旅人 1977
Description
深邃的星空可以被视作一张有向图,图上的节点就是点点恒星。点无点权,边有边权。图的点数为 ,边数为 ,图可能有重边自环。但保证至少有一条路径可以从 走到 (、 在输入中给定)。第 条有向边起点为 ,终点为 ,它的权值用一个有序三元组 表示。
莲子要从点 出发,经过了若干条边到达点 。她带有一个初始值均为 的长度为 的数组 ,每次经过编号为 的边,就会执行将 数组的区间 加 的操作。她使用了一棵带懒标记的线段树来维护这一操作。线段树的写法会在接下来给出。
你需要构造一条从 到 的路径,满足达到结点 时,其线段树上所有标记的和的最小。输出这个最小值。
以下是线段树的伪代码:(为了方便选手阅读,题目附件中给出了线段树的 C++ 源代码)
$$\begin{array}{l}\hline\hline\\[-0.8em] \textbf{Algorithm: }\text{SegTree}\\\hline\\[-0.5em] \begin{array}{rl} 1& \mathbf{Input.} \text{ 长度为 $k$ 的 $a$ 数组,初始全为 $0$}\\ 2& \mathbf{Output.} \text{ $a$ 数组进行若干次区间加操作后得到的结果}\\ 3& \mathbf{Method.}\\ 4& \mathrm{Add}(L,R,x)\\ 5& \quad\mathrm{Add0}(L,R,x,root,1,k)\\ 6& \mathrm{Add0}(L,R,x,u,l,r)\\ 7& \quad\mathbf{if}\ L \le l\ \mathbf{and}\ r\le R\\ 8& \quad\quad \mathrm{tag}(u) \gets \mathrm{tag}(u) + x\\ 9& \quad\quad \mathbf{return}\\ 10& \quad mid \gets \lfloor\frac{l+r} 2\rfloor\\ 11& \quad \mathrm{tag}(\mathrm{lson}(u)) \gets \mathrm{tag}(\mathrm{lson}(u))+\mathrm{tag}(u)\\ 12& \quad \mathrm{tag}(\mathrm{rson}(u)) \gets \mathrm{tag}(\mathrm{rson}(u))+\mathrm{tag}(u)\\ 13& \quad \mathrm{tag}(u) \gets 0\\ 14& \quad\mathbf{if}\ L \le mid\\ 15& \quad\quad\mathrm{Add0}(L,R,x,\mathrm{lson}(u),l,mid)\\ 16& \quad\mathbf{if}\ mid < R\\ 17& \quad\quad\mathrm{Add0}(L,R,x,\mathrm{rson}(u),mid+1,r)\\ \end{array}\\\hline\hline \end{array}$$Input Format
- 第一行五个整数 。
- 接下来 行,每行五个整数 。
Output Format
- 共一行一个整数,表示沿着你构造的路径从 到达 后线段树上所有懒标记的权值之和。
4 4 5 1 4
1 2 1 2 2
1 3 4 5 1
2 4 2 3 1
3 4 3 5 2
5
10 19 5 6 1
2 1 1 3 592
6 8 3 5 488
10 9 4 4 548
10 4 1 4 442
6 5 1 3 422
9 7 1 4 529
5 8 1 1 559
5 9 1 5 560
5 8 2 3 434
5 9 3 3 592
4 7 2 2 594
7 9 5 5 595
4 1 4 4 501
3 9 1 2 410
10 6 2 4 509
6 10 4 5 455
2 4 2 5 444
4 3 4 5 541
8 7 1 1 463
2295
Hint
样例解释
样例 #1
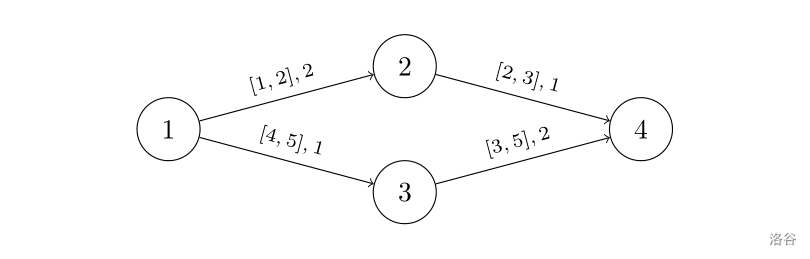
容易发现,样例 中有且仅有两条可能的路径: 与 。下面分别计算这两条路径最终 的权值和。
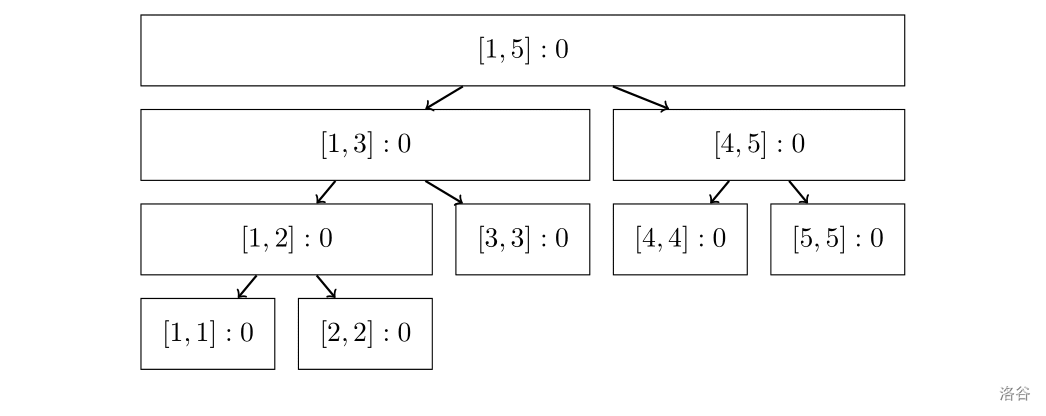
考虑画出这棵 的线段树。
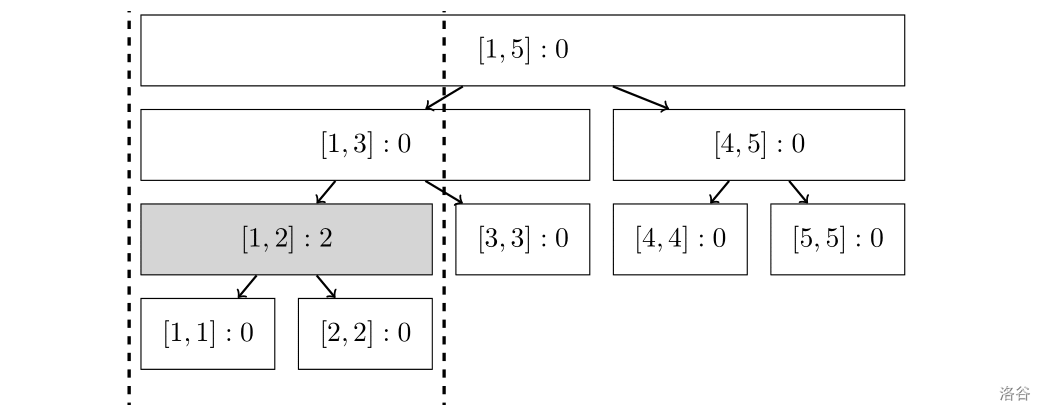
走了边 后, 节点被打上了权值为 的 。
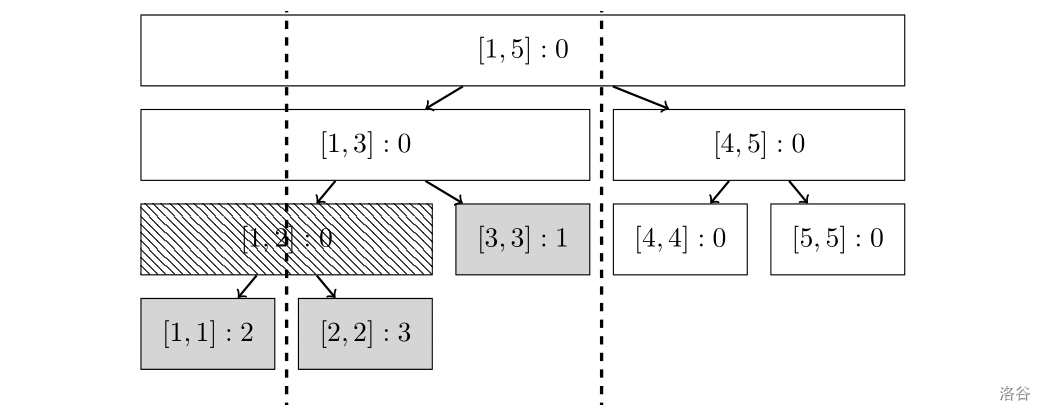
走了 后, 节点和 节点被打上了值为 的 ;但是 节点的标记进行了下推(因为使 区间 的时候会访问到 节点,而 ,故而发生标记下推),因此 节点和 节点的 分别加上了 ,最终成了如图所示的模样。
因此走到 之后所有结点的 之和为 。

对于另外一条路径,首先对 加上 。
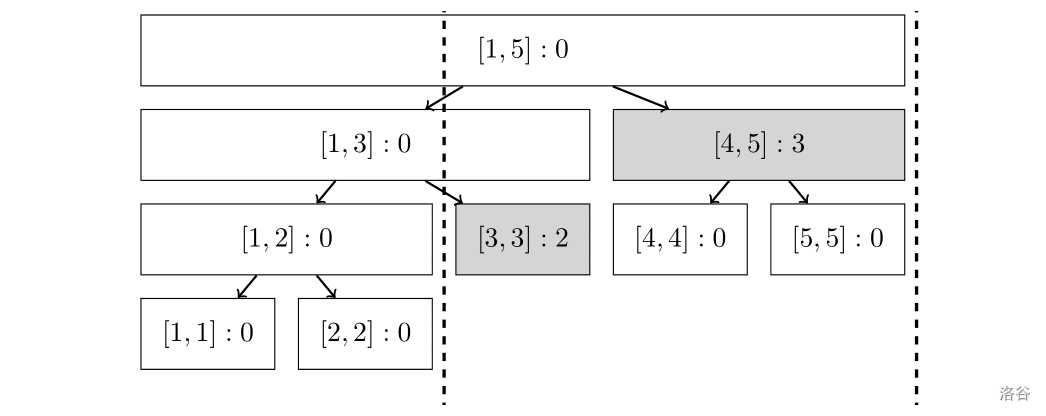
接着对 加上 。未发生带有 的节点的标记下推,因此最终的权值为 。
由于 ,因而最终的答案为 。
数据范围及约定
$$\def\arraystretch{1.5} \begin{array}{|c|c|c|c|c|c|c|}\hline \textbf{subtask}& \textbf{分值}& {\bm n\le} & {\bm m\le} & {\bm k\le} & \textbf{特殊性质} & \textbf{subtask 依赖}\cr\hline 1 & 10& 10 & 30 & 5 & - & -\cr\hline 2 & 5&30 & 30 & 12 & \textbf{AB} &-\cr\hline 3 & 20&30 & 500 & 12 & \textbf{B} &2 \cr\hline 4 & 15&200 & 3\times 10^3 & 25 & \textbf{B}&3\cr\hline 5 & 50&200 & 3\times 10^3 & 25 & - &4\cr\hline \end{array}$$- 特殊性质 :保证有且仅有一条从 到 的路径。
- 特殊性质 :保证图中不存在环。
对于 的数据,有 ,,,。
提示
在附件中有两个版本的线段树。 版本仅包含了在本题中你会用到的下推标记的操作,而标准版则较为完整地支持区间加、区间求和。选手可根据自己的喜好使用。

 京公网安备 11011102002149号
京公网安备 11011102002149号