题目背景

在 Cirno 的精心照料下，六边形成长为一只可爱的平行六边形。

现在，Cirno 很想知道它的战斗力是多少。

题目描述

可爱的平行六边形所有边的夹角均为 $\frac{2\pi}{3}$，三组对边的长度分别为 $a$，$b$，$c$ 个单位。如图。

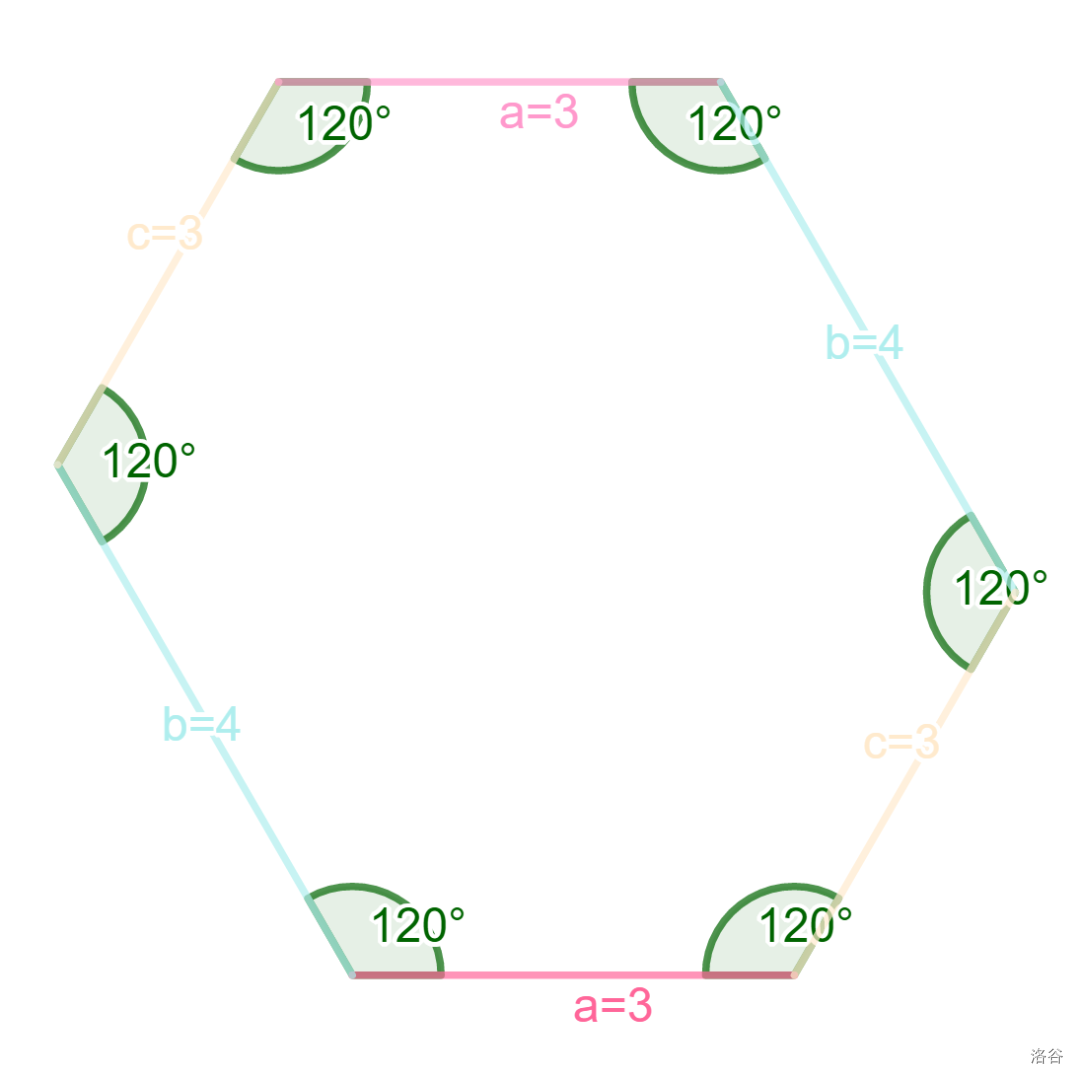
在战斗力鉴定时，鉴定师会以六边形的每一条边所在的直线，间隔 $\frac{\sqrt{3}}{2}$ 个单位建立平行直线系。这样六边形战士会被划分成若干个正三角形。如图。

鉴定师会将所有有公共边的正三角形连边。由于没有奇环，很容易知道这是一个二分图。然后鉴定师会试图构造该二分图的完美匹配。如图。

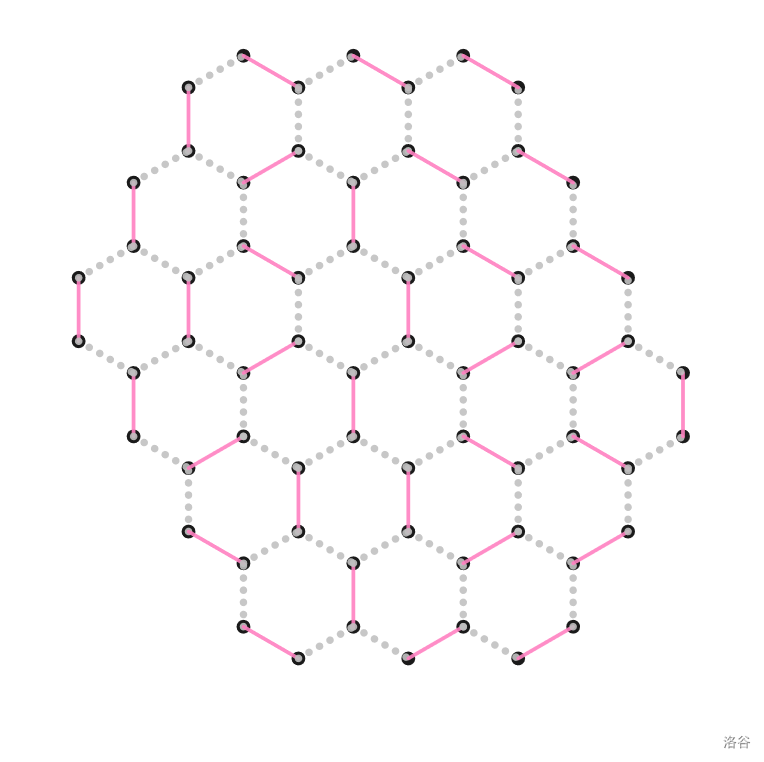
该六边形战士的战斗力为上述二分图的完美匹配可能的种类数。作为见习鉴定师，你需要帮 Cirno 求出该六边形的战斗力。

由于答案可能过大，仅需输出它对 $998244353$ 取模的结果即可。

输入格式

一行，三个整数，用空格隔开，表示 $a$，$b$，$c$。

输出格式

一行，一个整数，表示六边形战士的战斗力对 $998244353$ 取模后的结果。

1 1 1

2

3 4 3

4116

提示

数据范围与约定

对于 $100\%$ 的数据，保证 $1\le a,b,c\le 10^6$。

子任务

Subtask1（$10$ points）：$a,b,c\le 3$。

Subtask2（$10$ points）：$a,b,c\le 8$。

Subtask3（$70$ points）：$a,b,c\le 100$。

Subtask4（$10$ points）：无特殊限制。

提示

• Krattenthaler’s formula
  $\displaystyle\det\left(\prod\limits_{k=2}^j(x_i+a_k)\prod\limits_{k=j+1}^n(x_i+b_k)\right)_{i,j=1}^{n}=\prod\limits_{1\le i<j\le n}{(x_i-x_j)}\prod\limits_{2<i\le j\le n}(a_i-b_j)$。