题目描述

给定一张 $n$ 个点、$m$ 条边的无向图。边 $e$ 的长度为二元组 $(c_e, t_e)$。

一条途径 $w$ 的长度 $(c_w, t_w) = (\sum_{e \in w} c_e, \sum_{e \in w} t_e)$。

一条途径 $w$ 比另一条途径 $w'$ 短，当且仅当二者长度不同且 $c_w \le c_{w'}, t_w \le t_{w'}$。

显然可能有两条途径无法比较长短，进而两点间可能出现多条长度不同的最短路径。

求 $s$ 至 $e$ 的最短路径的长度取值的种类数。

输入格式

第一行四个整数 $n, m, s, e$。

接下来 $m$ 行，每行四个整数 $p, r, c, t$，分别表示一条边的两个端点与长度。

输出格式

一行一个整数，你的答案。

4 5 1 4 
2 1 2 1 
3 4 3 1 
2 3 1 2 
3 1 1 4 
2 4 2 4 

2 

提示

样例说明

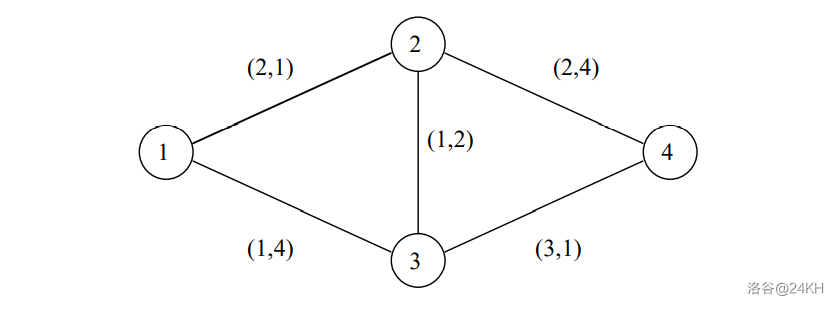
考虑其中四条途径：

0. $1 \to 2 \to 4$（长度为 $(4, 5)$）；
1. $1 \to 3 \to 4$（长度为 $(4, 5)$）；
2. $1 \to 2 \to 3 \to 4$（长度为 $(6, 4)$）；
3. $1 \to 3 \to 2 \to 4$（长度为 $(4, 10)$）。

途径 0、途径 1 均短于途径 3。最短路长度共有两种：$(4, 5)$（途径 0、途径 1）、$(6, 4)$（途径 2）。

数据范围

$1 \le s, e, p, r \le n \le 100$，$0 \le m \le 300$，$s \ne e$，$0 \le c, t \le 100$。

提示

BalticOI 2002 Day2 A.

由于自定义计分脚本参数配置，暂不支持 AC WA TLE MLE 外的评测状态显示。如果你得到了此外任何一种评测状态，你将得到 UKE。

Subtask #0 为样例；Subtask #1 为数据。