#P8046. [COCI 2015/2016 #4] CHEWBACCA
[COCI 2015/2016 #4] CHEWBACCA
Description
一棵 个节点的 级树是按照如下方式构造出来的:
- 首先,新建根节点,并将其编号为 。
- 随后重复如下步骤直至节点总数恰好为 :
- 设上一个新增节点的编号为 。
- 在上一层中从左往右找到第一个儿子个数 的节点。
- 如果该节点上没有儿子,则在该节点下新增一个儿子节点,编号为 ,并在点 和我们找到的该父亲节点之间连一条长度为 的边。
- 否则,在该节点最近添加的儿子节点的右边新增一个儿子节点,编号为 ,并在点 和我们找到的该父亲节点之间连一条长度为 的边。
- 如果在当前层没有找到儿子个数 的节点,则跳到下一层。
例如,下图为按照如上方法构造出来的包含 个节点的 级树:
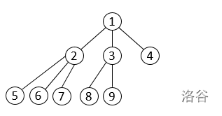
现在,你得到了这棵包含 个节点的 级树,你需要回答 次询问。每次询问给定两个整数 ,你需要回答在该树中节点 到节点 的最短路径长度。
Input Format
第一行输入三个整数 ,分别表示树的节点数、级数和询问次数。
随后 行,每行输入两个整数 ,表示本次询问的两个节点。
Output Format
输出 行,每行一个整数,表示节点 到节点 的最短路径长度。
7 2 3
1 2
2 1
4 7
1
1
4
9 3 3
8 9
5 7
8 4
2
2
3
Hint
【样例 1 解释】
下图是样例 1 中构造出来的树:

不难发现,对于第 、 次询问,由于节点 是节点 的儿子节点,因此这两个点之间的最短路径长度恰好为 。而对于第 次询问,一条最短路径是 $4\rightarrow 2\rightarrow 1\rightarrow 3\rightarrow 7$。因此其最短路径长度为 。
【样例 2 解释】
样例 2 构造出来的树见『题目描述』部分。
【数据范围】
对于 的数据,保证 。
对于 的数据,保证 。
对于所有数据,,,。
【题目来源】
本题来源自 COCI 2015-2016 CONTEST 4 T4 CHEWBACCA,按照原题数据配置,满分 分。
由 Eason_AC 翻译整理提供。

 京公网安备 11011102002149号
京公网安备 11011102002149号