题目描述

今天，Kile 在庆祝他的生日。他最好的朋友 Ivan 决定送给他一个特殊的天平。这种天平的特点是它是递归的，即在每个梁的末端，要么有一个砝码，要么有一个新的天平，要么什么都没有。当然，如果天平左梁上的总质量大于右梁上的总质量，则天平会向左倾斜。类似地，如果右侧梁上的质量较大，则天平向右倾斜。否则，我们说天平是平衡的。注意这里和我们平常所了解的天平的平衡条件是不同的。下图是一个该类天平的例子。

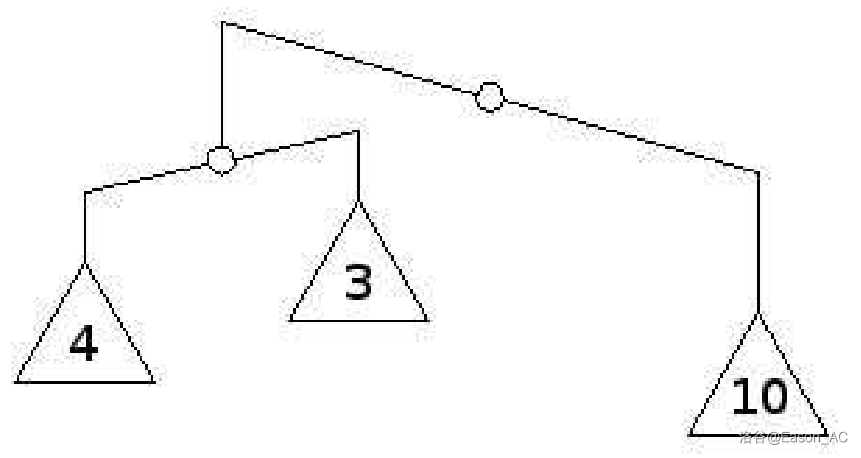
Kile 真的很喜欢这份礼物，作为一名真正的计算机科学家，他立即尝试使用总质量尽可能小的新的砝码来平衡这份礼物。新砝码的重量应该是正实数。如果某一个天平本身是平衡的，并且它的所有子天平都是平衡的，那么我们说这个天平是平衡的。

成功平衡天平后，Kile 决定在胸前纹上天平上砝码的总质量，以二进制表示，不带前导零。可以证明总质量必然是一个正整数。我们想知道 Kile 在胸前纹的的号码是多少，即以质量尽可能小的新的砝码来平衡这个天平之后，天平上所有砝码的总质量的二进制表示。

输入格式

第一行输入一个整数 $N$，表示天平里面包含的子天平数量。根天平的编号为 $1$。
随后 $N$ 行，第 $i$ 行两个整数 $a,b$，其中，如果 $a$ 是正数，那么就表示 $i$ 号天平左端是一个天平，否则表示 $i$ 号天平左端是一个质量为 $-a$ 的砝码；如果 $b$ 是正数，那么就表示 $i$ 号天平右端是一个天平，否则表示 $i$ 号天平右端是一个质量为 $-b$ 的砝码。

输出格式

输出仅一行，表示以质量尽可能小的新的砝码来平衡这个天平之后，天平上所有砝码的总质量的二进制表示。不包含前导零。

2
2 -10
-4 -3

10100

4
2 3
-9 4
-2 -13
-1 -7

111000

提示

【样例 1 解释】

天平的初始状态见题目描述中的图片。Kile 将会在 $2$ 号天平的左侧放一个质量为 $1$ 的砝码，右侧放一个质量为 $2$ 的砝码。此时，两个天平都处于平衡状态，可以证明这种方案增加的新的砝码的质量是最小的。此时，天平上所有砝码的总质量是 $5+5+10=20$，其二进制表示为 $10100$。

【数据范围】

对于所有数据，$1\leqslant N\leqslant 10^6$，$-10^9\leqslant a,b\leqslant N$。

【题目来源】

本题来源自 COCI 2016-2017 CONTEST 7 T4 POKLON，按照原题数据配置，满分 $120$ 分。

由 Eason_AC 翻译整理提供。