Description

为了更方便地描述题意，我们先给出以下定义：

• 子段：我们定义数组 $B$ 是数组 $A$ 从 $P$ 位置开始的子段，当且仅当 $|A| + P - 1 \le |B|$ 且 $B_1=A_P,B_2=A_{P+1},\dots,B_{|B|}=A_{P+{|B|}-1}$．
• 作为子段的出现次数：我们定义数组 $B$ 在数组 $A$ 中作为子段的出现次数为：初始设次数为 $0$．枚举每个不同的 $P$，若数组 $B$ 是数组 $A$ 从 $P$ 位置开始的子段，则将次数加一．最后得到的值即为数组 $B$ 在数组 $A$ 中作为子段的出现次数．
• 基因数组：每个细菌都有一个「基因数组」．它是一个值域为 $[1,k]$ 的整数数组．
• 目标数组：「目标数组」是一个值域为 $[1,k]$ 的整数数组．在本题中，我们会给定 $m$ 个不同的「目标数组」，第 $i$ 个数组为 $g_i$．
• 目标细菌：对于一个细菌，记它的「基因数组」为 $X$．我们统计每个「目标数组」$g_1, g_2, \dots, g_m$ 分别在 $X$ 中「作为子段的出现次数」，并将它们求和．若得到的和为 奇数，则我们称这个细菌为一个「目标细菌」．
• 基因突变：「基因突变」是作用于一个细菌的变换．给定一个 $k \times k$ 的突变概率矩阵 $p$．记这个细菌的「基因数组」为 $X$．对于 $x$ 中的每个元素 $X_i$，$X_i$ 会以 $p_{X_i,j}$ 的概率替换为 $j$（$1 \le j \le k$）．根据此定义，显然有 $\forall i \in [1,k], \sum_{i=j}^k p_{i,j}=1$．

一次实验的过程如下：

• 首先在一个空的培养皿中放入一个指定的细菌．
• 在接下来的每分钟，现有的每个细菌会分裂成两个细菌，每个细菌的「基因数组」与原细菌完全相同．分裂之后，每个基因都会进行一次「基因突变」．
• $t$ 分钟后，统计培养皿中「目标细菌」的数量，并结束实验．

现在给定一个长度为 $n$ 的「基因数组」$s$．对于 $s$ 的每个前缀数组 $s[1,1],s[1,2],\dots,s[1,n]$，假设该数组是实验开始时放入的细菌的「基因数组」，请你求出实验结束时得到的「目标细菌」的数量的期望，对 $10^9+7$ 取模．

Input Format

• 第一行输入四个整数，$n,m,k,t$．
• 第二行输入 $n$ 个整数，描述数组 $s$．
• 接下来输入 $m$ 行．每行第一个整数 $|g_i|$ 表示「目标数组」$g_i$ 的长度．接下来 $|g_i|$ 个整数描述「目标数组」$g_i$．
• 由于 $p$ 矩阵为实数矩阵，输入不方便，因此我们采用另一种方式输入 $p$ 矩阵．具体而言，接下来输入 $k$ 行，每行包含 $k$ 个整数，描述一个 $k \times k$ 的矩阵 $p'$．则有

$$p_{i,j}=\frac{p'_{i,j}}{\sum_{l=1}^k p'_{i,l}}.$$

Output Format

• 输出 $n$ 行，每行一个整数．表示假设以 $s[1,i]$ 为初始细菌的「基因数组」，实验结束后能得到的「目标细菌」的数量的期望，对 $10^9+7$ 取模．

2 2 2 1
1 1
1 1
2 2 2
1 1
1 1

1
500000005

5 5 5 1
1 4 2 3 3
3 1 1 4
3 5 1 4
4 1 4 1 4
2 5 3
1 5
9 9 8 2 4
4 3 5 3 2
1 4 7 4 8
3 6 4 7 1
1 4 5 1 4

250000002
273809526
931547626
97163867
377852186

Hint

样例解释

样例 #1

• 当前缀长度为 $1$ 时，初始细菌的「基因数组」为 $\{1\}$．分裂一次后变为 $\{1\}$ 和 $\{2\}$ 的概率均为 $\frac 1 2$．若变为 $\{1\}$，则是「目标细菌」；若变为 $\{2\}$，则不是「目标细菌」．分裂一次后培养皿中有 $2$ 个细菌，故「目标细菌」总数的期望为 $\frac 1 2\times 2=1$．
  
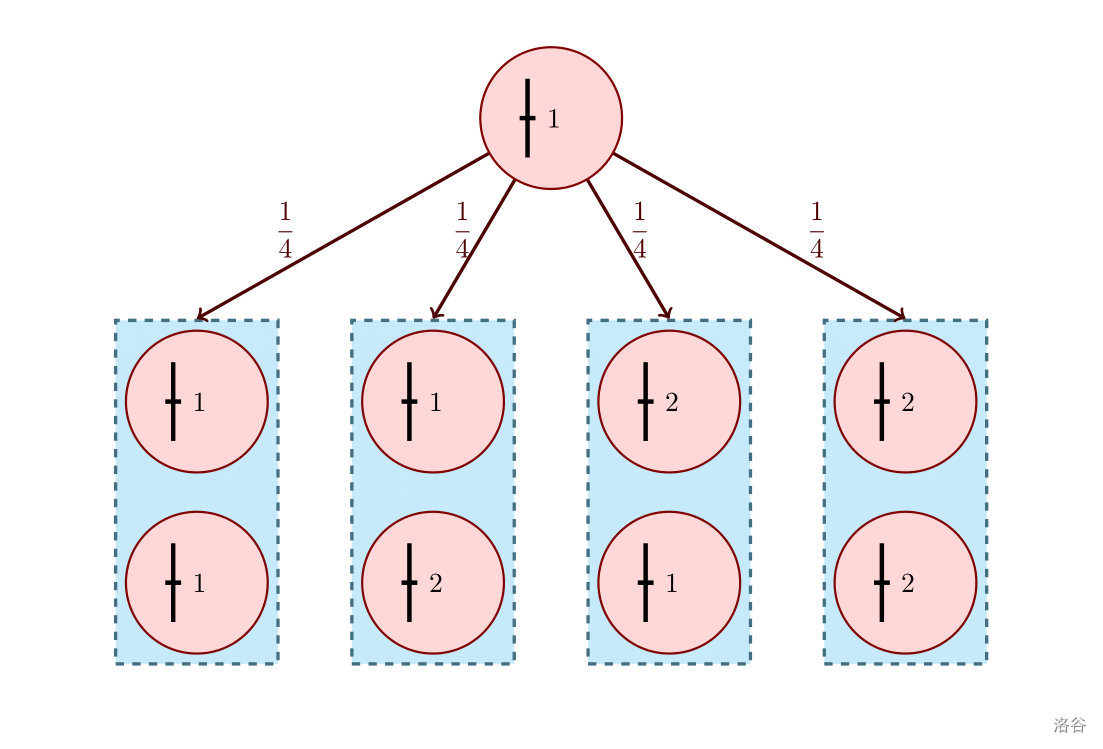
• 当前缀长度为 $2$ 时，初始细菌的「基因数组」为 $\{1, 1\}$．分裂一次后的细菌变为 $\{1, 1\}, \{1, 2\}, \{2, 1\}, \{2, 2\}$ 的概率都为 $\frac 1 4$．其中 $\{2, 2\},\{1,2\},\{2,1\}$ 均为「目标细菌」，$\{1,1\}$ 不是「目标细菌」（因为出现了两次子串 $\{1\}$）．即分裂后的「目标细菌」的总数的期望为 $\frac 3 4$．分裂一次后培养皿中有 $2$ 个细菌．即最后「目标细菌」数量之和的期望为 $\frac 3 4\times 2=\frac 3 2$．
  

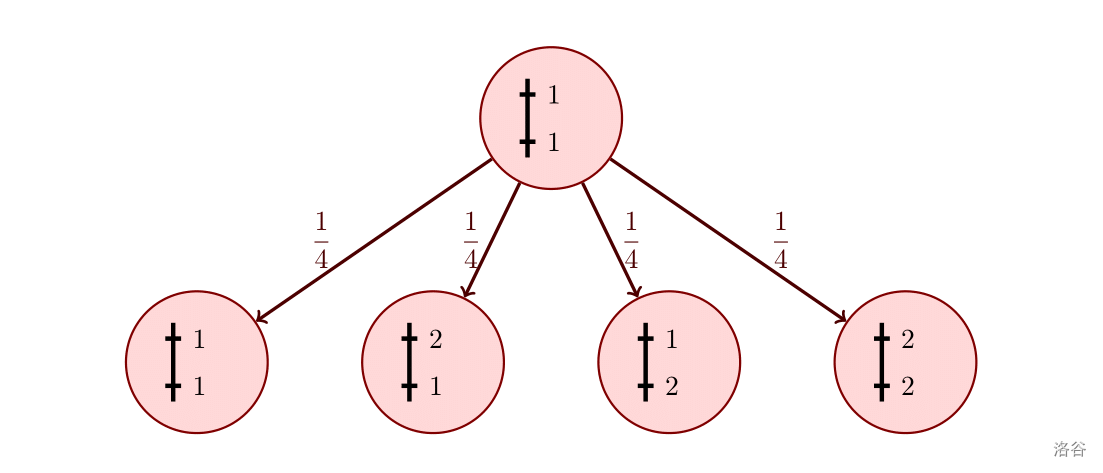
数据范围

本题采用捆绑测试，且不存在一个 Subtask 包含其他所有 Subtask 的数据范围和限制．

$$\def\arraystretch{1.5} \begin{array}{|c|c|c|c|c|c|c|c|} \hline \textbf{Subtask} & \textbf{分值} &\bm{n\le} & \bm{m\le} &\bm{k\le}&\bm{t\le} & \bm {|g_i|\le} & \textbf{特殊性质} \cr \hline 1 & 1 & 10^5 & 10^5 & 100 & 0 & 10^5 \cr \hline 2 & 14 & 5 & 5 & 5 & 1 & 5 \cr \hline 3 & 15 & 10^3 & 1 & 10^3 & 1 & 100 & \text{A} \cr \hline 4 & 30 & 5\times 10^4 & 5 & 10 & 1 & 50 & \text{B} \cr \hline 5 & 20 & 5\times 10^4 & 5 & 10 & 10^3 & 50 \cr \hline 6 & 20 & 10^3 & 10^4 & 10 & 10^3 & 10^4 & \text{C}\cr \hline \end{array}$$

• 特殊性质 $\textbf{A}$：对于 $i=1,2,\dots,m$，保证 $g_{i}$ 中所有整数均为 $1$
• 特殊性质 $\textbf{B}$：对于 $i=1,2,\dots, k$，$j=1,2,\dots,k$，保证 $p'_{i,j}=1$
• 特殊性质 $\textbf{C}$：保证 $\sum_{i=1}^m |g_i|\le 10^4$

对于所有数据，保证 $1\le n,m,\sum|g_i| \le 10^5$．$0\le t\le 10^3$，$0\le p'_{i,j} \le 10^9$．且 $p'$ 矩阵不会出现某一行的和在模 $10^9+7$ 意义下为 $0$．