#P8008. 「Wdsr-3」迷途竹林
「Wdsr-3」迷途竹林
Description
妖梦在迷途竹林里选定的竹子,可以看作在同一平面上。竹子可以看作有 根,每相邻两根竹子间距相等,并且每根竹子的倾斜程度相同。竹子的高度可以看作是无限高。
妖梦选定了一块多边形区域进行竹子的砍伐。只有在多边形内的部分才会被收集到。多边形共有 条边,为了防止出现歧义,保证任意一条边都不和竹子平行;保证多边形是简单多边形。
我们会使用两个实数 和 来描述这些竹子。这两个字母表示的含义可以参考下图:

现在妖梦需要知道她砍下来的竹子的总长度,也就是求出这些竹子(图中橙色的这些线段)的长度之和。
Input Format
- 第一行有一个正整数 ,表示多边形的边数。
- 接下来 行,将会按照顺时针顺序给出多边形的 个顶点的坐标,第 个点与第 个点连接 ,第 个点与第 个点连接。
- 接着给出描述线段的参数 和 。
Output Format
- 共一行,一个实数,表示所求得的竹子的总长。你的答案 被认为是正确的,当且仅当与标准答案 满足 $\dfrac{|\mathit{ans}-\mathit{std}\ |}{\max(1.0,\mathit{std}\ )}\le 10^{-6}$。
4
2.0000 2.0000
2.0000 -2.0000
-2.0000 -2.0000
-2.0000 2.0000
45.0000 1.0000
22.6274169980
8
0.0000 2.5000
1.0000 1.5000
2.5000 1.0000
2.0000 -1.0000
1.0000 -2.0000
-2.0000 -2.0000
-2.5000 1.0000
-1.0000 2.0000
60.0000 0.8000
23.1662217484
Hint
样例 1 解释
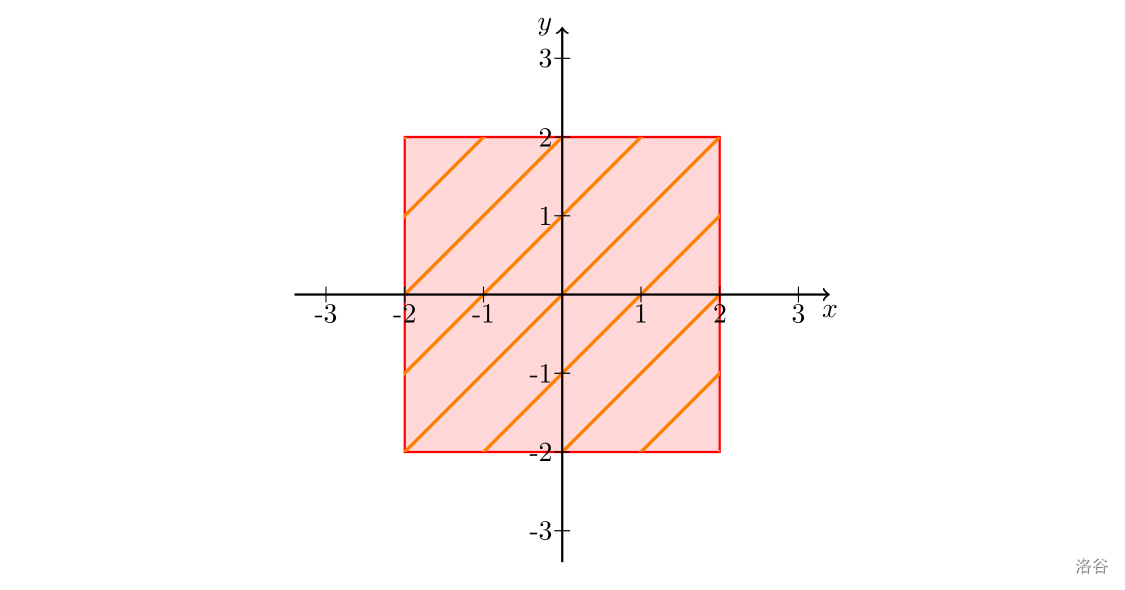
容易发现,竹子总长(即橘红色线段的总长度)为 。
样例 2 解释

我有一个精妙绝伦的方法解释样例 ,可惜这里空白太小写不下。
数据范围及约定
$$\def\arraystretch{1.5} \begin{array}{|c|c|c|c|}\hline \textbf{Subtask} & \bm{n\le} & \textbf{特殊性质} & \textbf{分值}\cr\hline 1 & 10 & \text{A} & 30 \cr\hline 2 & 10^3 & - & 20 \cr\hline 3 & 10^5 & \text{B} & 20 \cr\hline 4 & 10^5 & - & 30 \cr\hline \end{array}$$特殊性质 :保证 。
特殊性质 :保证 。
- 对于 的数据,保证 $3\le n\le 10^5;|x_i|,|y_i|\le 10^4;\theta\in[1,179);a\in[0.1,100]$。输入数据当中出现的浮点数均保留四位小数。

 京公网安备 11011102002149号
京公网安备 11011102002149号