题目描述

The only difference between the two versions is whether you have to find a way to get the maximum points.

Cirno drew a graph. This graph contains $4\cdot n$ nodes, numbered $0$ through $4\cdot n - 1$. Also:

• For any $0\le i\le 3$ and $0 \le j, k \lt n$, node $(n\cdot i + j)$ and node $(n\cdot i + k)$ are connected.
• For any $0 \le i < n$ and $0 \le j, k \le 3$, node $(i + n\cdot j)$ and node $(i + n\cdot k)$ are connected.

Cirno called Daiyousei to come and play with her.

The rules for this game are as follows:

• Firstly, Cirno chooses $2\cdot n$ (i.e. half) of the nodes, and she colors them blue. The rest are left red.
• Then there are $2\cdot n$ turns: for each turn Cirno first chooses a blue node, and Daiyousei chooses a red node. If those two nodes are connected, Daiyousei gets a point.

Try to maximize the number of points Daiyousei gets.

输入格式

The first line contains an integer $n$. Then one line below, $2\cdot n$ numbers follow: they are the nodes that Cirno chose.

输出格式

For each test case, output an integer $x$ in a single line, which is the maximum number of points Daiyousei can get.

You don't have to output anything else in this version.

题目大意

两个难度之间的唯一区别为是否需要输出对应的匹配方案

给定 $4n$ 个点，点的编号从 $0$ 到 $4n-1$，每个点有两种属性 $x$ 和 $y$，编号为 $i$ 的点的属性为 $x_i=\left\lfloor\frac{i}{n}\right\rfloor,y_i=i-n\left\lfloor\frac{i}{n}\right\rfloor$。对于每两个点 $i,j(0\le i <j < 4n)$ 之间，若 $x_i= x_j$ 或 $y_i= y_j$，则这两点有一条无向边相连。现有其中 $2n$ 个不同的点被选择，试给每个被选择的点都匹配上另一个点，使得：

• 被匹配到的点未被选择；
• 每个点都只被匹配一次；
• 若每个点与其匹配的点之间有连边，那么记为一分，需要最大化分值。

请输出最大的分值。

3
0 1 2 3 4 5

6

提示

Explanation

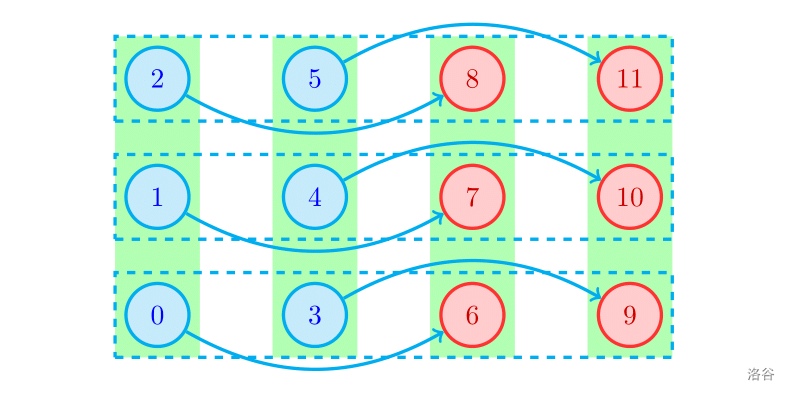
In the following picture, nodes in matrices are connected to each other. Cirno chose nodes $0,1,2,3,4,5$.

Arrows below show a possible way for Daiyousei to get the maximum number of points she can get.

Constraints

$1\le n\le 2\times 10^6$.