题目背景

建议先看 E 题题目背景。

题目描述

对于一个 $1\sim n$ 的排列 $p$，定义 $G_p$ 为使用以下方法构造出来的无向图：

• 对于每一个 $i\in (1,n]$，找到最大的 $j\in [1,i)$ 满足 $p_i>p_j$，然后连一条 $i,j$ 之间的边，如果不存在这样的 $j$ 则不连。

给定一棵有 $n$ 个节点的树 $T$。

把 $p$ 称为好排列当且仅当 $G_p$ 与 $T$ 同构。

如果存在好排列，输出其中字典序最大的一个。否则输出 $-1$。

无向图 $G_1,G_2$ 同构当且仅当存在一个 $1\sim n$ 的排列 $q$，满足 $\forall (u,v)\in G_1,(q_u,q_v)\in G_2,\forall (u,v)\notin G_1,(q_u,q_v)\notin G_2$。

输入格式

第一行，一个整数 $n$。

接下来 $n-1$ 行，每行两个整数 $u,v$，表示 $u,v$ 之间有一条边。

输出格式

共一行，$n$ 个整数，表示答案；或一个数 $-1$，表示无解。

5
1 2
1 3
2 4
2 5

1 5 4 2 3

9
1 2
2 3
1 4
4 5
5 6
1 7
7 8
8 9

1 9 2 6 7 8 3 4 5

提示

对于 $100\%$ 的数据，$1\le u,v\le n\le 5\times 10^3$。

	分值	$n$	特殊性质
$\operatorname{Subtask}1$	$15$	$\le 8$	无
$\operatorname{Subtask}2$	$5$	无特殊限制	树退化为一条链
$\operatorname{Subtask}3$	$15$		度数 $\ge 3$ 的节点个数 $\le 1$
$\operatorname{Subtask}4$	$20$	$\le 100$	无
$\operatorname{Subtask}5$		$\le 10^3$
$\operatorname{Subtask}6$	$25$	无特殊限制

说明：样例解释中的节点编号是 $p$ 中的下标。

样例解释 1

$G_p$ 的形态如下：

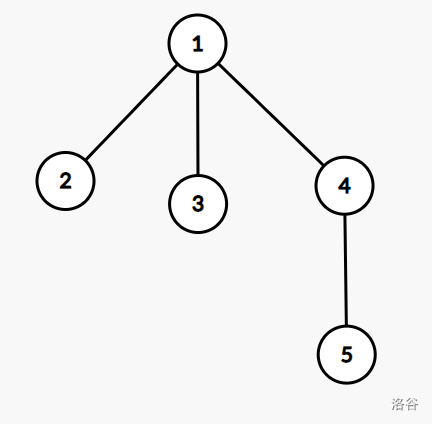
可以证明没有更优的方案。

样例解释 2

$G_p$ 的形态如下：

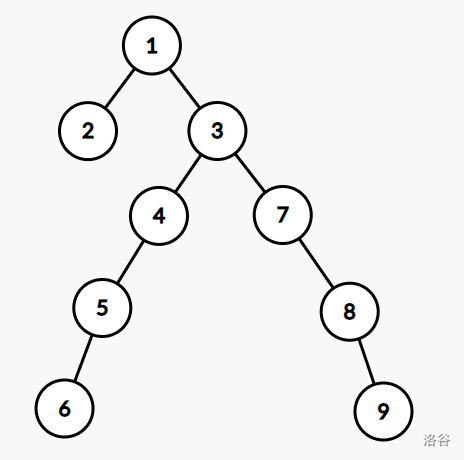
可以证明没有更优的方案。