#P7841. 「C.E.L.U-03」100%不公平的游戏
「C.E.L.U-03」100%不公平的游戏
Description
这个游戏是在树上进行的。Bob 先手。Bob 和 Al 轮流进行以下操作,首先无法操作者判负。
- 在树上标记一条未被标记过的边。满足在每一次操作之后,存在一条简单路径遍历所有标记过的边。注意:这条简单路径可以经过未标记过的边。
如果给定的树对于 Bob 有必胜方案,输出 Play now,否则输出 Restart。
Input Format
本题多测,第一行输入一个整数表示数据组数 。
对于每组测试数据,第一行输入一个整数 表示树的节点数。
接下来 行,每行输入两个整数 表示 是树上的一条边。
Output Format
对于每组测试数据,输出一个字符串,大小写敏感。
2
9
9 5
2 1
9 8
3 2
5 6
7 9
4 3
5 2
3
1 2
2 3
Play now
Restart
附加两组样例详见
https://www.luogu.com.cn/paste/b6mh7ido
附加两组样例详见
https://www.luogu.com.cn/paste/b6mh7ido
Hint
样例数据也可见附件 。
样例解释 1
第一组数据:
先手选择边 必胜:
若后手选择 ,先手选择 可以获胜。
若后手选择 ,先手选择 可以获胜。
若后手选择 ,先手选择 可以获胜。
若后手选择 ,先手选择 可以获胜。
若后手选择 ,先手选择 可以获胜。
若后手选择 ,先手选择 可以获胜。
若后手选择 ,先手选择 可以获胜。
综上,无论后手选那一条边,都不会获得胜利。
第二组数据:
先手不存在必胜策略:
若先手选择 ,后手选择 获胜。
若先手选择 ,后手选择 获胜。
样例解释 2
各组数据详见下图,其中前两组数据与样例一相同。
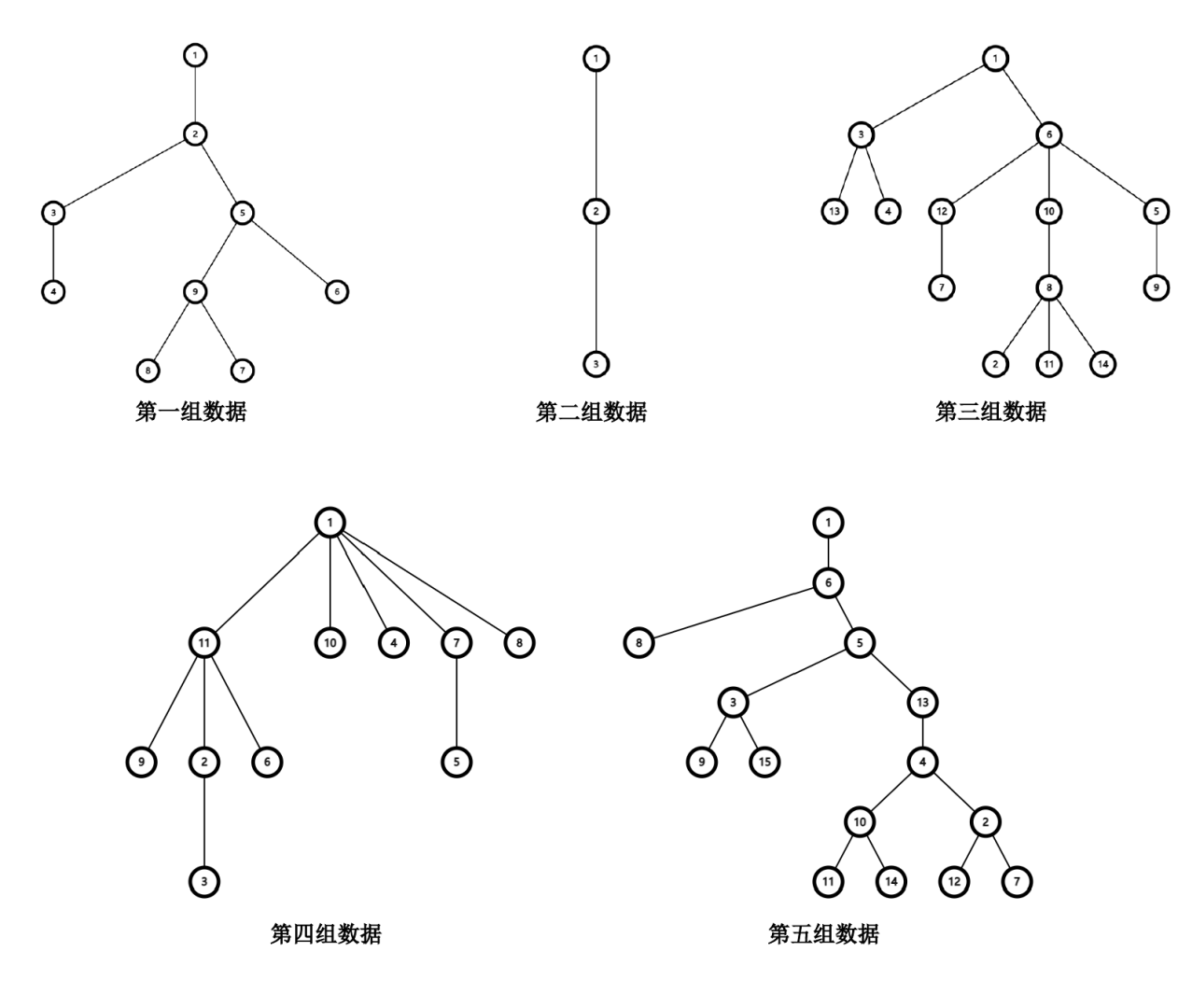
数据范围
数据保证给定的图是一棵树。
子任务
- (8分)。
- (18分)。
- (6分) 。
- (8分)。
- (30分)。
- (6分)最多存在两个节点度数大于 。
- (12分)树的形态是一棵完全二叉树。
- (12分)无特殊性质。

 京公网安备 11011102002149号
京公网安备 11011102002149号