#P7676. [COCI 2013/2014 #5] TROKUTI
[COCI 2013/2014 #5] TROKUTI
Description
给定 条在平面直角坐标系内的直线,这些直线上的点满足 。
请你求出这些直线围出的三角形个数,答案对 取模。
保证没有三线共点。
Input Format
第一行,一个整数 ,表示直线条数;
接下来 行,每行 个 ,表示直线 满足的条件。
Output Format
一个整数,表示这些直线围出的三角形对 取模后的个数。
6
0 1 0
-5 3 0
-5 -2 25
0 1 -3
0 1 -2
-4 -5 29
10
5
-5 3 0
-5 -3 -30
0 1 0
3 7 35
1 -2 -1
10
Hint
【样例解释 #1】
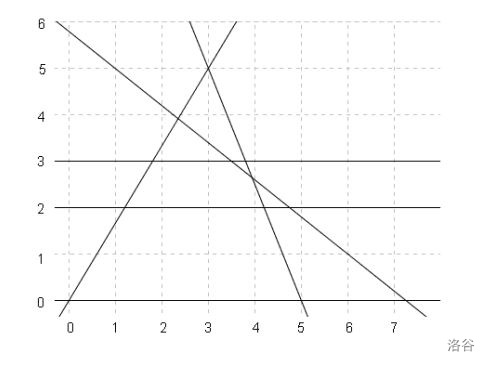
上图即为所有直线在平面直角坐标系上的位置,共围出了 个三角形。
【数据范围】
对于 的数据,,。
【说明】
本题分值按 COCI 原题设置,满分 。
题目译自COCI2013_2014 CONTEST #5 *T5 TROKUTI

 京公网安备 11011102002149号
京公网安备 11011102002149号