#P7600. [APIO2021] 封闭道路
[APIO2021] 封闭道路
Description
在泗水市,有 个路口(编号从 到 )。这些路口由 条双向道路连接(编号从 到 ),因此通过这些道路,任意一对路口之间都有一条唯一的路径。 号道路()连接着 号和 号路口。
为了提高环保意识,泗水市长 Pak Dengklek 计划举办无车日。为了鼓励该活动,Pak Dengklek 将组织封路。Pak Dengklek 将首先选择一个非负整数 ,然后封闭一些道路,以使每个路口只能直接连接至多 条未封闭的道路。封闭 号道路的成本为 。
请你帮助 Pak Dengklek 对每个可能的非负整数 ()计算封闭道路的最低总成本。
你需要实现下列函数:
int64[] minimum_closure_costs(int N, int[] U, int[] V, int[] W)
-
:泗水市的路口数量。
-
和 :大小为 的数组,其中 号路口和 路口通过 号道路直接连接。
-
:大小为 的数组,其中封闭 号道路的成本为 。
-
该函数需要返回一个大小为 的数组。对每个 (), 号元素是使得每个路口与至多 条未封闭道路直接连接的最低总成本。
该函数将被调用恰好一次。
Input Format
示例测试程序按如下格式读取输入数据:
- 第 行:
- 第 ()行:
Output Format
示例测试程序输出仅一行,包含一个数组,表示 minimum_closure_costs 的返回值。
5
0 1 1
0 2 4
0 3 3
2 4 2
10 5 1 0 0
4
0 1 5
2 0 10
0 3 5
20 10 5 0
Hint
例子
例子
考虑如下调用:
minimum_closure_costs(5, [0, 0, 0, 2], [1, 2, 3, 4], [1, 4, 3, 2])
这个例子中共有 个路口和 条道路,分别连接着路口 和 ,封闭它们的成本依次为 和 。
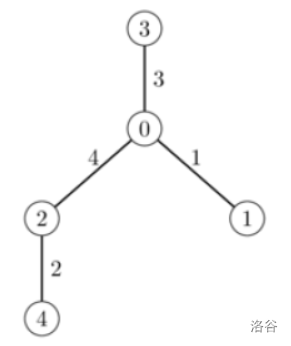
为了得到最低的总成本:
- 如果 Pak_Dengklek 选择 ,那么所有道路都需要封闭,总成本为 ;
- 如果 Pak_Dengklek 选择 ,那么需要封闭 号道路和 号道路,总成本为 ;
- 如果 Pak_Dengklek 选择 ,那么需要封闭 号道路,总成本为 ;
- 如果 Pak_Dengklek 选择 或 ,那么没有道路需要封闭。
因此,minimum_closure_costs 应该返回数组 。
例子
考虑如下调用:
minimum_closure_costs(4, [0, 2, 0], [1, 0, 3], [5, 10, 5])
这个例子中共有 个路口和 条道路,分别连接着路口 和 ,封闭它们的成本依次为 和 。
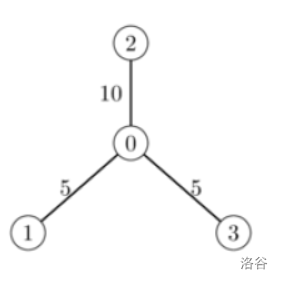
为了得到最低的总成本:
- 如果 PakDengklek 选择 ,那么所有道路都需要封闭,总成本为 ;
- 如果 PakDengklek 选择 ,那么需要封闭 号道路和 号道路,总成本为 ;
- 如果 PakDengklek 选择 ,那么需要封闭 号道路或 号道路,总成本为 ;
- 如果 PakDengklek 选择 ,那么没有道路需要封闭。
因此,minimum_closure_costs 应该返回数组 。
约束
- 任意一对路口可以通过道路互相到达。
- 。
子任务
- (5 分)
- (7 分) ,
- (14 分)
- (10 分)
- (17 分)
- (25 分)
- (22 分) 无附加限制

 京公网安备 11011102002149号
京公网安备 11011102002149号