题目背景

本题只支持 C++ 提交，提交时不需要包含 hexagon.h 头文件，只需要将附件中的 hexagon.h 中的内容粘贴到代码的开头即可。

题目描述

对于一个用六边形无限平铺的平面，Pak Dengklek 站在其中一个格子上，并称该格子为初始格子。如果六边形平铺中的两个格子有公共边，则称它们是相邻的格子。对于一步移动，Pak Dengklek 可以从一个格子向六个可能的方向（从 $1$ 到 $6$ 编号，如下图所示）移动到与其相邻的格子上。

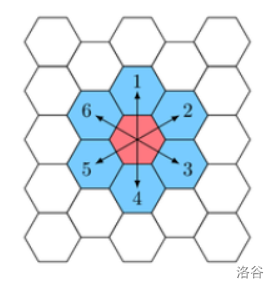
对于某个由 $N$ 次行动构成的行动序列，Pak Dengklek 可以用其产生的路径（对应一个按序访问的格子序 列）构造一个领域。其中第 $i$ 次行动由移动方向 $D[i]$ 和在该方向上的移动步数 $L[i]$ 组成，并且该路径应有如下性质：

• 路径是 封闭 的，这意味着在格子序列中，起点格子与终点格子（即初始格子）相同。
• 路径是 简单 的，这意味着在格子序列中，除了初始格子访问过恰好两次（起点和终点分别访问一 次），其他格子只能被访问至多一次。
• 路径是 暴露 的，这意味着在格子序列中，每个格子与至少一个不在序列中出现过的非 内部格子 相邻。
  • 如果一个格子不在格子序列中出现过，并且从它出发，在不经过格子序列中任何格子的情况下，（通过若干步移动） 只能访问到有限个格子，我们就称该格子是 内部格子 。

下图是一个符合上述条件的路径例子。其中：

• $1$ 号格子（粉色）是初始格子。
• 被编号的格子（淡蓝色）组成格子序列，编号代表它被访问的顺序。
• 被标上叉号的格子（深蓝色）是 内部格子。

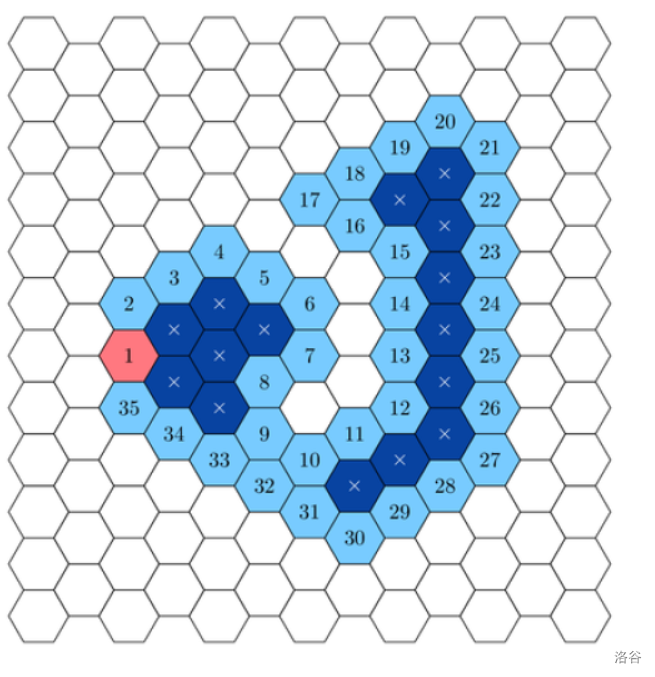
构造出的领域只包含所有路径上的格子和内部格子。领域中格子 $c$ 的距离定义为：在只经过领域中包含格子的情况下，从初始格子出发到达 $c$ 所需要的最少移动步数。领域中一个格子的分数定义为 $A+d \times B$，其中 $A$ 和 $B$ 是 Pak Dengklek 给定的常数，$d$ 是该格子在领域中的距离。下图给出了用上示路径构成的领域中每个格子的距离。

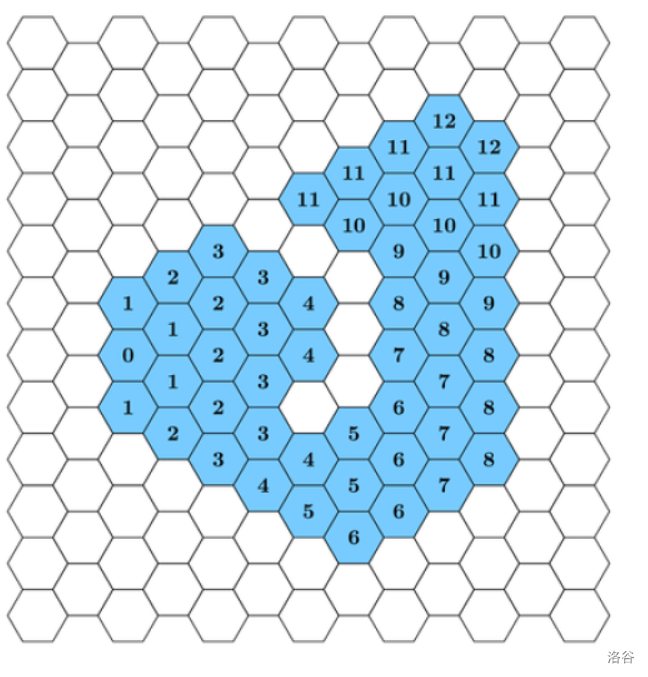
请帮助 Pak Dengklek 计算，用给出的行动序列构成的领域中，所有格子的分数之和。由于总分数值可能很大，最终结果对 ${10}^9+7$ 取模。

你需要实现下列函数：

int draw_territory(int N, int A, int B, int[] D, int[] L)

• $N$：行动序列中行动的次数。
• $A,B$：分数计算中的常数。
• $D$：大小为 $N$ 的数组，其中 $D[i]$ 表示第 $i$ 次行动的方向。
• $L$：大小为 $N$ 的数组，其中 $L[i]$ 表示第 $i$ 次行动的移动步数。
• 函数应该返回用给出的行动序列所构成的领域中，所有格子的分数总和对 ${10}^9+7$ 取模后的值。
• 该函数将被调用恰好一次。

输入格式

示例测试程序按如下格式读取输入数据：

• 第 $1$ 行：$N$ $A$ $B$
• 第 $2+i$（$0 \le i \le N-1$）行：$D[i]$ $L[i]$

输出格式

示例测试程序按如下格式输出你的答案：

• 第 $1$ 行：draw_territory 的返回值。

17 2 3
1 2 3 4 5 4 3 2 1 6 2 3 4 5 6 6 1
1 2 2 1 1 1 1 2 3 2 3 1 6 3 3 2 1

1003

提示

【样例解释】

考虑下列调用：

draw_territory(17, 2, 3,
			   [1, 2, 3, 4, 5, 4, 3, 2, 1, 6, 2, 3, 4, 5, 6, 6, 1],
			   [1, 2, 2, 1, 1, 1, 1, 2, 3, 2, 3, 1, 6, 3, 3, 2, 1])

该行动序列和上述题面中给出的例子相同。下表列出了该领域中所有可能的距离值所对应的分数。

距离值	格子数	每个格子分数	总分数
$0$	$1$	$2+0 \times 3=2$	$1 \times 2=2$
$1$	$4$	$2+1 \times 3=5$	$4 \times 5=20$
$2$	$5$	$2+2 \times 3=8$	$5 \times 8=40$
$3$	$6$	$2+3 \times 3=11$	$6 \times 11=66$
$4$		$2+4 \times 3=14$	$4 \times 14=56$
$5$	$3$	$2+5 \times 3=17$	$3 \times 17=51$
$6$	$4$	$2+6 \times 3=20$	$4 \times 20=80$
$7$		$2+7 \times 3=23$	$4 \times 23=92$
$8$	$5$	$2+8 \times 3=26$	$5 \times 26=130$
$9$	$3$	$2+9 \times 3=29$	$3 \times 29=87$
$10$	$4$	$2+10 \times 3=32$	$4 \times 32=128$
$11$	$5$	$2+11 \times 3=35$	$5 \times 35=175$
$12$	$2$	$2+12 \times 3=38$	$2 \times 38=76$

总分数值为 $2+20+40+66+56+51+80+92+130+87+128+175+76=1003$。

因此，draw_territory 应该返回 $1003$。

【数据范围】

• $3 \le N \le 2\times {10}^5$。
• $0 \le A,B \le {10}^9$。
• $1 \le D[i] \le 6$（$0 \le i \le N-1$）。
• $1 \le L[i]$（$0 \le i \le N-1$）。
• $L$ 中的元素之和不超过 ${10}^9$。
• 给出的行动序列所对应的路径一定是 封闭、简单 和 暴露 的。

【子任务】

1. （3 分）：$N=3$，$B=0$。
2. （6 分）：$N=3$。
3. （11 分）：$L$ 中的元素之和不超过 $2000$。
4. （12 分）：$B=0$，$L$ 中的元素之和不超过 $2\times {10}^5$。
5. （15 分）：$B=0$。
6. （19 分）：$L$ 中的元素之和不超过 $2\times {10}^5$。
7. （18 分）：$L[i]=L[i+1]$（$0 \le i \le N-2$）。
8. （16 分）：无附加限制。