#P7558. [JOISC 2021] 曲芸飛行 (Day1)
[JOISC 2021] 曲芸飛行 (Day1)
Description
在一个平面直角坐标系上,有 个点 ,小 B 从一个点出发,任意选择一个点作为终点走直线路径过去,并重复这个过程 次,不难发现这个过程会形成由 条线段组成的折线,除了第一个点和最后一个点之外的每一个点都会形成一个夹角 (小于等于 的那个角, 即代表第 个经过的点),小 B 要求你通过策划折线路径经过的点的顺序求得下面这个式子的最大值:
Input Format
第一行两个整数 代表点数和评分参数(见下方数据规模与约定和评测说明)。
接下来 行每行两个整数 代表一个点。
Output Format
行每行一个整数 代表第 个经过的点的编号。
7 90
3 1
2 5
0 2
-1 6
-3 1
-1 -4
4 -2
5
3
1
7
6
4
2
Hint
样例 1 解释
如下图所示:
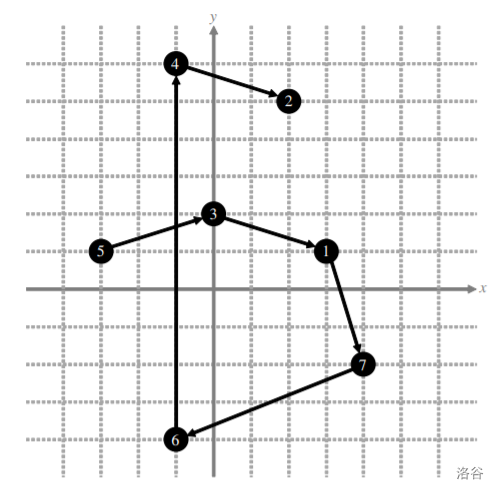
最小的夹角在点 处,为 ,根据 和下方评测方式中的评分参数说明,这个输出可以得到 的分数。
数据规模与约定
对于 的数据,,,任意两点不重合,。
具体地,本题为提交答案题,共有 个测试点:
- 输入文件为
input_01.txt到input_06.txt。 - 输出文件为
output_01.txt到output_06.txt。 - 每一个测试点的 , 和分数分别为:
| 测试点编号 | 分数 | ||
|---|---|---|---|
评测参数
本题采用 Special Judge。
感谢 @035966_L3 提供的 Special Judge。
如果您的输出格式有误或者输出的数不是 等其他错误,您抱铃。
如果您的输出格式是正确的,假设您得到的最小夹角是 ,则您的分数如下:
- 如果 ,您将得到满分。
- 如果 ,设该测试点分数为 ,您将得到 。
定义函数 为:
评测库
我们额外提供评测库(在文件 aerobatics.h 中),您可以用他计算三个点形成的夹角度数。
调用格式如下:
double GetAngle(int xb,int yb,int xa,int ya,int xc,int yc)或double GetAngle(int xb,int yb,int xc,int yc,int xa,int ya)- 这个函数计算 ,误差足够小。
- 请保证顺序正确。
- 为点 。
- 为点 。
- 为点 。
- 如果 或 ,那么,嘿,嘿嘿。
附加文件说明
- 名称:下方附件中的
aerobatics-dist.zip。- in & out:样例输入输出。
- aerobatics.h:评测库。
- 名称:下方附件中的
aerobatics-data.zip:- in:输入数据。
说明
翻译自 第20回日本情報オリンピック 春季トレーニング合宿 Day1 A 曲芸飛行 (Aerobatics) 的英文版本。

 京公网安备 11011102002149号
京公网安备 11011102002149号