#P7359. 「JZOI-1」旅行
「JZOI-1」旅行
Description
这次旅行是在一个由 个城市和 条双向道路组成的一个国家中,其中保证任意两个城市可以互达。
为了美化环境,所有道路都是沿河修建的,这意味着小僖可以自己制造一艘船,然后划船通过这条路,所以小僖每走一条边都可以从陆上走过去,也可以划船通过。
当然,因为顺流和逆流的原因,所以有一个参数 ,换句话讲,如果从陆上走过这条边所花费的时间为 ,那么顺流而下划船所花费的时间为 (保证结果大于 ),逆流而上花费的时间为 。不过,造船需要 的时间,且人一旦上了岸,就必须放弃这条船只。
现在小僖想你帮忙算一下从 走到 的最短时间。
注意:一条船可以连续走多段水路(只要你不下船)
Input Format
第一行三个数,。
接下来 行,每行五个数,,其中 表示水从 流向 , 表示水从 流向 。
接下来 行,每行两个数 ,表示每个计划的起点和终点。
Output Format
行,每行一个数,表示每一个询问的答案。
3 2 2
1 2 2 1 0
1 3 3 2 1
2 3
1 2
4
2
4 1 1
1 2 100 99 1
2 3 100 99 0
3 4 100 99 1
1 4
104
Hint
样例1解释
图长这样:
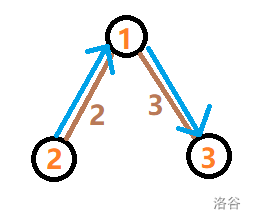
对于第一组询问,也就是从 到 ,我们可以在 号节点造船,花费 的时间,然后从节点 顺流而下到 ,花费 ,在顺流而下到 ,花费 ,所以总花费为 。
数据范围
对于 的数据,。
对于另外 的数据,树的形态随机。
对于另外 的数据,所有的 或所有的 都相等。
最后一个测试点给出了一条链。
对于 的数据,,且 。

 京公网安备 11011102002149号
京公网安备 11011102002149号