题目背景

lhm 最近迷上了国际象棋，他对里面的骑士最感兴趣，于是就开辟了下面这个玩法。

题目描述

lhm 现在建立了一个大小为 $n \times m$ 的国际象棋棋盘，你作为白方要与黑方作战。棋盘上黑方只有一个国王，国王位置不会移动，而 lhm 有无穷无尽的骑士。现在你需要解出，最少派出几个骑士才能将死黑方国王，定义将死的标准为黑方国王在不被吃掉的情况下不能移动为止。

更形式化地讲：一个 $n\times m$ 的棋盘上有一个国王，你需要摆放尽可能少的骑士在棋盘上，使得对于每一个国王能走正好一步达到的且不在棋盘外的位置，都存在至少一个骑士能走正好一步达到。

棋子的移动方法：

国王每一步能向上、下、左、右、左上、右上、左下、右下八个方向移动一格。

骑士与国际象棋规则相同，每次可以走日字（即 $2\times3$ 长方形的对角线，详见样例）。注意没有蹩马腿规则，也就是只要不走出棋盘且按照日字格行走，其他没有限制。

lhm 太菜了，只好请聪明的你来帮他完成这个任务。

输入格式

本题有多组数据。

第一行一个整数 $T$，表示数据组数。

对于每组数据，一行四个整数 $n,m,x,y$，表示棋盘大小和黑方国王的坐标。

输出格式

输出共 $T$ 行，每行一个整数，表示最少派出骑士的个数。

1
8 8 1 1

2

2
10 9 1 9
999 999 999 2

2
3

提示

【样例1解释】

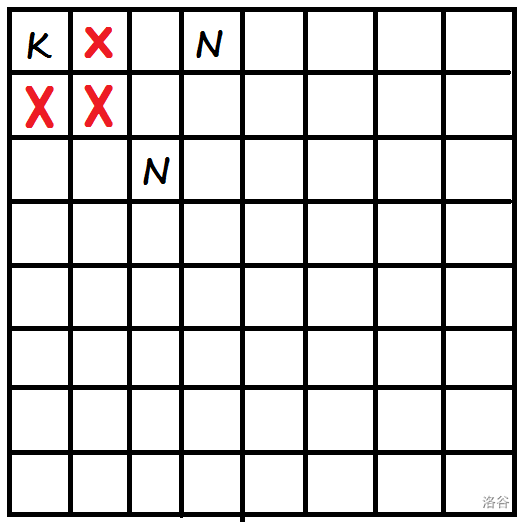
一个类似上图的棋盘，$\text{K}$ 表示黑方国王，$\text{N}$ 表示白方骑士，$\color{red}{\times}$ 表示骑士可以到达的地方（其中 $(3,3)$ 的 $\text{N}$ 封住了 $(1,2)$ 和 $(2,1)$，$(1,4)$ 的 $\text{N}$ 封住了 $(2,2)$ ，形如上图，$\text{K}$ 已经被封死了，所以两个骑士足矣。可以证明两个骑士是最小个数。

【数据范围】

• 对于 $30\%$ 的数据，保证国王的初始位置一定在棋盘最外面一圈。

• 对于 $100\%$ 的数据满足，$1 \leq t \leq 10$，$1 \leq x,y \leq 10^9$，$8 \leq n,m \leq 10^9$。