题目描述

令 $G$ 为一个有向无环图。如果 $c_1,c_2,c_3,\cdots,c_n$ 满足有一条从 $c_1$ 到 $c_2$ 的路径，有一条从 $c_2$ 到 $c_3$ 的路径，……且有一条从 $c_{n-1}$ 到 $c_n$ 的路径，我们就称数组 $C=(c_1,c_2,c_3,\cdots,c_n)$ 为一从 $c_1$ 开始，$c_n$ 结束的有序数组。注意在相邻元素 $c_i$ 和 $c_{i+1}$ 之间不必直接相连，只需有一条路径存在即可。

我们定义有序数组 $C=(c_1,c_2,c_3,\cdots,c_n)$ 的长度为 $\text{len}(C)=n$。因此，一个有序数组的长度等同于它包含的顶点个数。注意有序数组的长度可以仅为 $1$，此时它仅包含一个顶点。该顶点将既是数组的开头，又是结尾。

同时，对于一个有序数组 $C=(c_1,c_2,c_3,\cdots,c_n)$，我们定义它的符号为 $\text{sgn}(C)=(-1)^{\text{len}(C)+1}$。对于 $G$ 中的顶点 $x,y$，我们用 $S_{x,y}$ 表示所有以 $x$ 开头并以 $y$ 结尾的有序数组的集合。

最后，我们定义顶点 $x$ 和 $y$ 的矛盾度为 $\text{tns}(x,y)=\sum_{C \in S{x,y}} \text{sgn}(C)$。因此，顶点 $x$ 和 $y$ 的矛盾度等同于所有以 $x$ 开头并以 $y$ 结尾的有序数组的符号之和。

给定一个整数 $K$。你的任务是构造一个最多有 $1000$ 个点，$1000$ 条边的有向无环图，使得 $\text{tns}(1,N)=K$。其中，$N$ 表示图中顶点的个数。图中的顶点应当依次从 $1$ 到 $N$ 编号。

输入格式

第一行，输入一个整数 $K$。

输出格式

第一行，输出所构造的有向无环图的顶点个数 $N$ 和边的条数 $M$。

接下来的 $M$ 行中，第 $i$ 行，输出两个不同的整数 $X_i$ 和 $Y_i$，代表第 $i$ 条边将连接 $X_i$ 和 $Y_i$。每条边在输出中仅能出现一次。

并且，你的方案中任何两个顶点之间的矛盾度不得超过 $2^{80}$。

如果有多种方案，请输出任意一种。

0

6 6
1 4
1 5
4 3
5 3
3 2
2 6

1

1 0

2

6 8
1 2
1 3
1 4
1 5
5 4
2 6
3 6
4 6

提示

样例 #1 解释

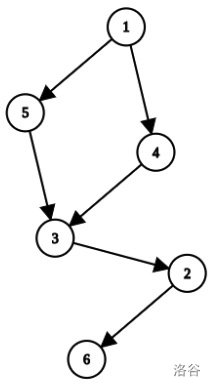
样例构造的图有 $6$ 个顶点。以 $1$ 开始，以 $6$ 结尾的有序数组有：$(1,6),(1,4,6),(1,5,6),(1,3,6),(1,2,6),(1,4,3,6),(1,4,2,6),(1,5,3,6),(1,5,2,6),(1,3,2,6),(1,4,3,2,6),(1,5,3,2,6)$。它们的长度分别为 $1,2,2,2,2,3,3,3,3,3,4,4$，所以对应符号分别为 $−1,1,1,1,1,−1,−1,−1,−1,−1,1,1$。因此，$1$ 和 $6$ 之间的矛盾度等于 $−1+1+1+1+1−1−1−1− 1−1+1+1=0$。

数据规模及约定

子任务编号	分值	数据范围及约定
$1$	$15$	$1 \le K \le 500$
$2$		$-300 \le K \le 1$
$3$	$20$	$\lvert K \rvert \lt 10000$
$4$	$60$	无

对于 $100\%$ 的数据，$\lvert K \rvert \le 10^{18}$，输出中的数据满足 $1 \le N \le 1000$，$0 \le M \le 1000$，$1 \le X_i,Y_i \le N$。

说明

本题分值按 COCI 原题设置，满分 $110$。

本题的 Special Judge 改自 LOJ 3268，文件详见附件。

题目译自 COCI2019-2020 CONTEST #6 T3 Konstrukcija 。