题目背景

  众目睽睽之下被要求解锁另一个人的手机是一件非常恐怖的事。

  ——特别是密码关于自己的时候。

---

  被堆在讲台周围乌压压的同学围着，小灰毛表示自己真的很难。作为班长的阿绫被叫去开会，存着月考名次表的手机被交给天依保管。但消息不出意料地走漏，现在一班觊觎着分数数据的饿狼一致要求天依打开手机……

  “真不知道密码啊！”拖延着，心里早就猜到手势密码的答案。

  最后，试探而肯定地划出一个字母“Y”，解锁成功。什么意思呢？首先排除“依”的首字母。

  这个时候肯定有起哄的啦！

  “懂的都懂~”“别问，问就是 XX即是正义！”……

题目描述

乐正大小姐用的手机很高级，所以她的手势密码也很花哨。

具体地，现在有一棵 $n$ 个结点的树，对于两个结点 $u,v$，当且仅当 $(u,v)$ 是一条树边时，手势才能从其中一个点（$u$ 或 $v$）划向另一个点（$v$ 或 $u$）。更奇怪的是，这种手势密码不限制仅划一次，但每次划出的路径必须是树上的一条简单路径。

现在阿绫告诉了天依在她的密码中每个结点被手势划过的次数（作为手势的起点或终点也算划过一次），其中第 $i$ 个结点划过 $a_i$ 次。那么，天依至少要划多少次才能解开密码呢？

---

简化题意

有一棵带点权的树。定义一次操作为选择树上的一条简单路径，并将这条简单路径上的所有点点权减去 $1$。问至少需要多少次操作，使树上所有点的点权恰好变为 $0$。

输入格式

第一行一个整数 $op$，表示数据输入方式类型。

如果 $op=1$：

第二行一个正整数 $n$，表示结点个数。

第三行 $n$ 个非负整数 $a_1,a_2,\cdots,a_n$，表示每个结点的点权。

接下来 $n-1$ 行，每行两个正整数 $u,v$，表示一条连接结点 $u$ 和结点 $v$ 的树边。

如果 $op=2$：

我们将给出一个输入的模板：

#include <cstdio>
int a[3000005], u[3000005],v[3000005];
namespace Generate{
	int n,seed;
	static const int mod=1e9;
	int Rand(int x){
		seed=(1ll*seed*0x66CCF+19260817ll)%x+1;
		seed=(1ll*seed*0x77CCF+20060428ll)%x+1;
		seed=(1ll*seed*0x88CCF+12345678ll)%x+1;
		seed=(1ll*seed*0x33CCCCFF+10086001ll)%x+1;
		return seed;
	}
	void RS(int* a, int* u, int* v){ //你需要传入三个参数，分别表示点权，一条边的两个端点 
		int cnt=0;
		for(int i=1;i<=n;i++)a[i]=Rand(mod); 
		for(int i=2;i<=n;i++){
			int fa=Rand(i-1);
			cnt++;
			u[cnt]=fa,v[cnt]=i;
		}
	}
};
int main () {
	int op;
	scanf("%d",&op);
	if(op==1){
		//直接输入 
	}else{
		int n;
		scanf("%d %d",&Generate::seed,&n);//输入种子和n 
		Generate::n=n;//记得赋值 
		Generate::RS(a,u,v); //开始工作 
	}
	return 0;
}

第二行两个整数 $seed$ 和 $n$，表示生成器的种子与结点个数。

输出格式

一行一个整数，表示最少的操作次数。

1
4
1 2 1 2
1 2
2 3
2 4

2

1
8
1 4 2 8 5 7 8 1
1 2
2 3
2 4
2 5
1 6
6 7
6 8

19

2
10086001 100000

26892182890608

提示

样例解释 2

给出的树形态如下，括号中的数字表示该点的点权。

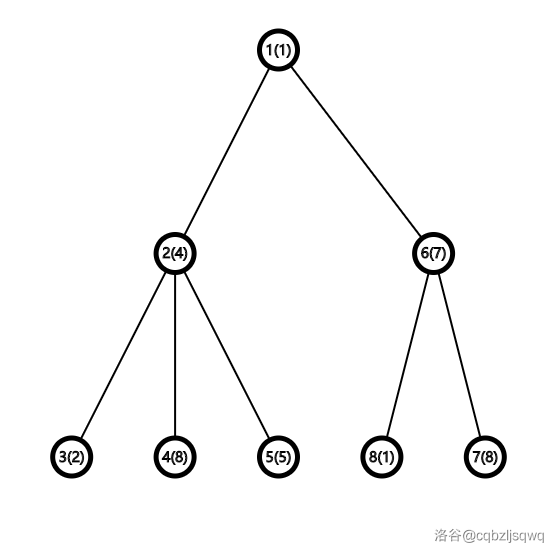
一种最优的操作方案为 $(3,4)\times2,(4,5),(4,4)\times4,(5,5)\times4,(4,7),(7,8),(6,7)\times6$。其中 $(u,v)$ 表示对从 $u$ 到 $v$ 的简单路径进行一次操作。

---

数据规模与约定

本题采用捆绑测试。

对于 $100\%$ 的数据，$op\in\{1,2\}$，$1\le seed\le 10^9$，$1\le n\le 3\times 10^6$，$0\le a_i\le10^9$，$1\le u,v\le n$，保证 $u\ne v$。

子任务	分值	$op$	$n$	$a_i$	特殊性质
1		$1$	$2$	/	/
2	4		$3$
3	10		$\leq 6$	$\leq 3$
4	5		$\leq 10^6$	/	A
5	15		$\leq 50$		/
6	5		$\leq 5\times 10^3$	$\leq 100$	B
7	10		$\leq 10^5$
8				/	C
9				$\leq 100$	/
10	30	/

• 特殊限制 A：对于第 $i$ 条边 $(u,v)$，保证 $u=i,v=i+1$。
• 特殊限制 B：输入的边构成一棵满二叉树。
• 特殊限制 C：对于 $\forall 1\le i\le n$ 有 $a_i=1$。

---

提示

Subtask 10 时限 2S。

对于 $op=2$ 的数据，输入的模板只用于减小输入量，标程不依赖该数据生成方式。

【2024.7.2 补充】

的数据生成器生成的树形并没有随机性。（因为在生成 $2$ 的父亲时，最终 seed 一定会变为 $1$，此后的随机序列就完全相同了。）这一点不影响数据的正确性，但导致数据强度下降，我们为此致歉。鉴于本题提交较多，不做题面和数据修改。