题目描述

Bobi 每天早上起床喂他最喜欢的宠物：蚂蚁。他把它们放在一个有管道系统的玻璃瓶中，管道系统可以表示为一棵有 $n$ 个节点的树。管道用树的边缘表示。树的根位于用 $1$ 表示的节点上。在管道系统内部，由于重力的作用，液体从节点流向其子节点。我们知道每个管道的流量 $x_i$：从父节点到子节点的流量百分比。让我们观察以下示例：

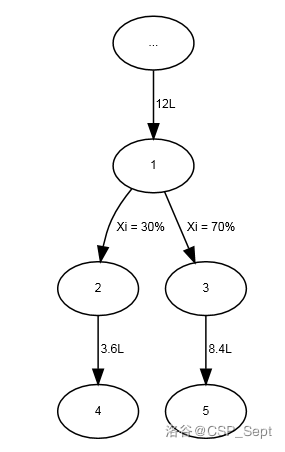
图片中的节点 $1$ 有 $12$ 升液体，之后有两个管道。一个的流量是 $x_i=30$，另一个是 $x_i=70$。节点 $2$ 将得到 $3.6$ 升，节点 $3$ 得到 $8.4$ 升。在输入数据中，来自同一节点的管道流量之和始终等于 $100$。Bobi 的一些管子不只是普通的管子，它们有点奇怪。它们是超级管道，有超能力将流经它们的液体流量平方。在前面的例子中，如果第一个管道有超能力，节点 $2$ 得到 $12.96$ 升，节点 $3$ 仍然只有 $8.4$ 升。现在请注意，一个节点的流出液体比进入的液体多。这正是这些管道是超级管道的原因！

所有的超级管道都可以由波比开启或关闭。蚂蚁只生活在树的叶子里（没有孩子的节点）。对于每一片叶子，我们知道需要多少液体来喂养生活在叶子里的蚂蚁。Bobi 想把 $L$ 升液体倒进树根里喂蚂蚁。他没有多少钱，所以他想知道他需要购买的最低液体量，以保证所有蚂蚁的饲料。

输入格式

第一行输入包含整数 $n$。

以下 $n-1$ 行中的每一行包含四个整数 $a_i,b_i,x_i,t_i$，其中 $a_i$ 和 $b_i$ 是管道的末端（管道连接的节点的编号），$x_i$ 是液体通过管道的流量，$t_i$ 表示管道是否具有超能力。如果 $t_i$ 为 $1$，则该管道具有超能力，否则它不具有超能力。

下一行包含 $n$ 个整数 $k_i$，用于描述第 $i$ 个节点中蚂蚁所需的液体量。如果第 $i$ 个节点不是叶，$k_i$ 将是 $-1$。

输出格式

仅一行，即 $L$。

注意：本题采用 SPJ，与正确解的误差不超过 $10^{-3}$ 即视为正确。

5
1 2 50 0
1 3 50 0
2 4 25 0
2 5 75 1
-1 -1 4 1 9

8.00

3
1 2 20 1
1 3 80 1
-1 4 8

10.0000

6
1 2 100 1
2 3 20 0
2 4 20 0
2 5 60 0
4 6 100 1
-1 -1 1 -1 1 2

2.659

提示

样例 1 说明

如果 Bobi 向根节点中注入 $8$ 升液体，节点 $3$ 得到 $4$ 升，节点 $4$ 得到 $1$ 升，节点 $5$ 得到 $9$ 升。这些节点是叶子（其中有蚂蚁）中蚂蚁需要得到的最小数量。所以，$8$ 升是满足“蚂蚁”条件的最低液体量。

数据规模与约定

对于 $100\%$ 的数据，都有 $1\le n\le 10^3$，$1\le a_i,b_i\le n$，$1\le x_i\le 100$，$t_i\in\{0,1\}$，$k_i\in[1,10]$。

数据保证 $L$ 的值不超过 $2\times 10^9$。

说明

题目译自 COCI2014-2015 CONTEST #4 T4 MRAVI。