#P6853. station
station
Description
你需要规划一个城市的公交路线。
总共有 条路线和 个车站,编号均从 开始。
你的主要任务是,规划每一条路线应该经过哪些车站。换言之,你要任意选择一个车站的子集,让这条路线经过这个子集中的所有车站。
定义两条路线是关联的,当且仅当它们经过了同一个车站,也就是它们的经过车站集合有交。
一个路线方案必须满足如下限制:
-
一条线路不可能只通过一个车站,所以每条线路至少要经过两个车站;
-
一个车站的运载能力是有限的,所以一个车站最多只能被三条线路经过。
-
为了保证交通顺畅,对于任意两条不同线路 ,都存在第三条线路 ,使得 与 均关联。
现给定 ,请求出一个最小的 和具体规划方案。
Input Format
一行一个正整数 ,含义如题目所示。
Output Format
第一行输出一个正整数 ,表示在你的规划方案中所用车站的数量。
接下来 行中,第 行输出一个正整数 和若干个正整数 ,表示在你的方案中第 条路线经过的车站数目以及经过车站的编号。
4
4
2 1 2
2 2 4
2 2 3
3 1 3 4
Hint
「样例 1 解释」
如图所示。
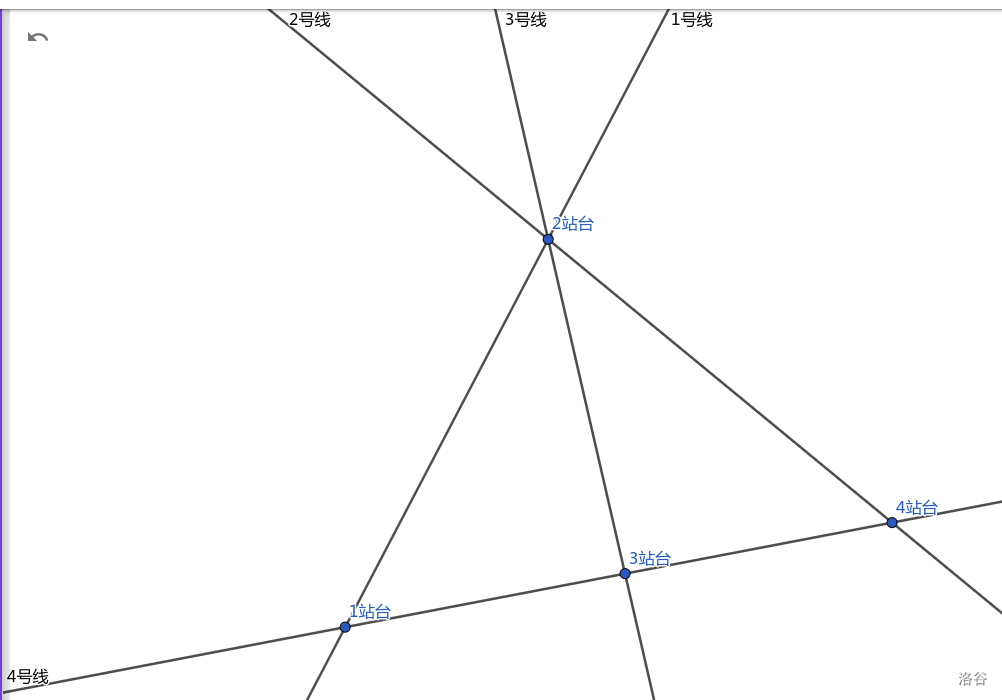
首先易知其满足题目描述中所给定的一、二条件。下面考虑三条件。
先考虑 号线,可以发现这三条线路构成了一个三角形,任意两个线路均有剩下的一条线路与它们关联;
再对 号线与 号线分别考虑,容易验证满足对于任意 ,均有另一条线路 与 同时关联,满足题目条件。
「Special Judge 说明与评分细则」
请认真阅读输出格式。
如果你的输出出现了如下情况,将会被判为 分:
- 输出格式不符。如没有正确换行,输出了一些奇奇怪怪的字符,未输出车站个数等。
- 某一条线路经过了相同的车站,或者有某一个车站的编号不在 内。
- 没有满足题目描述中所给定的三条限制。
- 输出文件大小过大或者是 过大。如果你的 大于 将直接判为 分。输出文件过大将导致 TLE 或 OLE,建议将输出文件大小控制在 25Mb 以内。
在没有被判为 分的基础上,将会根据你输出的 的大小进行判分。
每个测试点评测时会有 个评测参数 ,若你输出的 小于等于其中 个参数,那么你将得到该测试点 的分数。
这 个参数是对外不可见的,也即你的程序在运行时无法获知这些评测参数。
「数据范围」
本题采用捆绑测试。你在某个 subtask 的得分为在该 subtask 的所有测试点中的最小得分。
- Subtask 1(20 points):。此处我们保证 个评分参数均为 。
- Subtask 2(40 points):。
- Subtask 3(40 points):无特殊限制。
对于所有数据,均满足 ,且 $ans + 5 \le w _1 \le w _2 \le \cdots \le w _{10} = 10 ^6$,其中 表示标准答案。
请注意此处的 的条件。

 京公网安备 11011102002149号
京公网安备 11011102002149号