Description

春季大扫除也许是我们一生中最无聊的事情之一。当然，对于 Flóra 和她的母亲而言，今年的春季大扫除要有意思得多。因为她们在地毯下发现了一张已被灰尘覆盖的树形地图。

这棵树有 $N$ 个节点，节点从 $1$ 到 $N$ 进行编号，这 $N$ 个点通过 $N-1$ 条边相连。这些边上都积累了过多的灰尘，因此 Flóra 的母亲准备对这棵树进行清理。

清理这棵树的过程是这样的：Flóra 的母亲每次在这棵树上选择两个叶子节点（定义一棵树的叶子节点为只与恰好一个点直接相连的点），并对这两个叶子点路径上的所有边进行清理。如果这条路径上有 $d$ 条边，则清理的费用为 $d$。当这棵树上的所有边都被清理后，这棵树的清理过程就完成了。清理这棵树的总费用即为各次清理的费用之和。

因为她想保护这棵树的叶子节点，因此对于每个叶子节点，她最多只会选择一次。

Flóra 认为原来的树过于简单，她决定对原始的树进行一些改造。在第 $i$ 次改造中，她在原始的树的基础上添加了 $D_i$ 个叶子节点。具体来说，她会在原始的树上选择一个节点，并在该点与新的叶子节点之间连接一条边。需要注意的是，在添加新的叶子节点的过程中，原来的一些节点将不再是叶子节点。

现在你需要帮助 Flóra 求出清理改造后的树的最小费用。

Input Format

输入第一行包含两个数 $N,Q$，分别代表原始的树上的节点数，以及 Flóra 准备对原始的树进行的改造次数。

接下来 $N-1$ 行，每行两个整数 $u,v$，表示在原始的树上 $u,v$ 两个节点间有一条边相连。

接下来 $Q$ 行，每行第一个整数 $D_i$，表示 Flóra 准备在第 $i$ 次改造中添加 $D_i$ 个叶子节点。接下来 $D_i$ 个整数，第 $j$ 个整数 $a_j$ 表示 Flóra 准备在 $a_j$ 号点上添加一个叶子节点。同一个点上可能会添加多个叶子节点。

每次改造过程是独立的，即在一轮改造后，Flóra 会在原始的树上重新开始改造过程。

Output Format

对于每次改造，你需要输出一个整数，表示清理这棵改造后的树的最小费用。

特别地，若这棵树不能被完全清理，输出 $-1$。

7 3
1 2
2 4
4 5
5 6
5 7
3 4
1 4
2 2 4
1 1

-1
10
8

Hint

样例解释

下面展示的是第二次改造后的树：

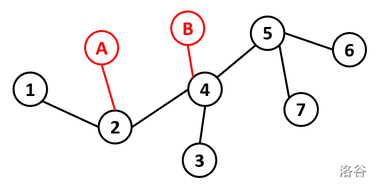
一种最优的清理方案是清理 $1-6$，$A-7$，$B-3$ 这三条路径上的所有边。

子任务

所有测试点均满足：$3 \leq N \leq 10^5$，$1 \leq Q \leq 10^5$，$\sum D_i \leq 10^5$，$1 \leq u,v \leq N$，$1 \leq a_j \leq N$。

各子任务的约束条件如下：