#P6748. 『MdOI R3』Fallen Lord
『MdOI R3』Fallen Lord
Description
L 国有 个城市,它们之间有 条道路,形成了一棵树的结构。
国王 L 派遣了一些军队来驻守这些道路,驻守每一条道路的军队战斗力都可以被量化为 中的整数。
每个城市都有一个城主,第 个城主有一个忍耐度 。如果国王 L 在与第 个城市相连的所有道路上驻守的军队战斗力的中位数超过了城主的忍耐度,那么城主就会认为国王不信任他而产生谋反的心理。
国王 L 当然不希望有人造反,但他又想使驻守道路的军队的总战斗力最大来保证国防安全。现在他找到了 L 国最强的 OIer —— 您,去来帮助他解决这个问题。
如果无论如何安排军队都会有人想要造反,那么输出 -1。
注:对于任意 个数,它们的中位数是将这些数从小到大排序后第 个数。
Input Format
第一行两个正整数,表示 。
第二行 个整数,第 个数表示 。
接下来 行,每行两个数 ,表示一条直接连接城市 与城市 的道路。
输入数据保证构成一棵树。
Output Format
一行一个整数,表示最大的总战斗力。
7 100
50 25 25 12 12 12 12
1 2
1 3
2 4
2 5
3 6
3 7
148
Hint
更多样例请到这里领取。
对于所有数据,,,。
| 子任务编号 | 其他性质 | 分值 | ||
|---|---|---|---|---|
| 1 | 无 | |||
| 2 | ||||
| 3 | 树的形态为一条链 | |||
| 4 | 存在度数为 的节点 | |||
| 5 | 每个节点度数 | |||
| 6 | 无 | |||
| 7 | ||||
其中,留空的表示和 的数据范围限制相同。
样例解释
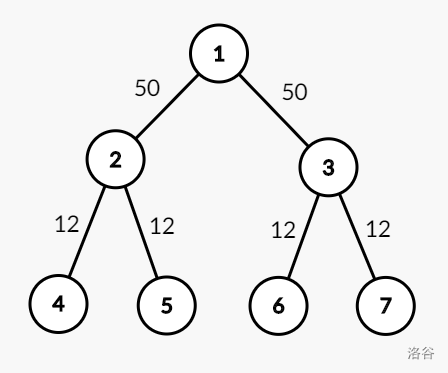
如图驻守 条道路的军队战斗力(按照输入中的顺序)依次为 。

 京公网安备 11011102002149号
京公网安备 11011102002149号