#P6658. 边三连通分量
边三连通分量
Description
给出一个 个点, 条边的无向图 ,,请求出其所有的极大边三连通分量。
Input Format
第一行输入两个整数 ,表示点数、边数。
接下来 行,每行输入两个数 ,表示图上的一条边。
Output Format
第一行输出一个整数 ,表示极大边三连通分量个数。
接下来输出 行,每行若干整数,表示一个极大边三连通分量内所有点。
对于单个极大边三连通分量,请将点按照标号升序输出。对于所有极大边三连通分量,请按照点集内编号最小的点升序输出。
4 5
1 3
1 2
4 1
3 2
3 4
3
1 3
2
4
17 29
1 2
1 10
1 10
2 3
2 8
3 4
3 5
4 6
4 6
5 6
5 6
5 7
7 8
7 11
7 12
7 17
7 17
8 9
9 10
11 12
11 17
12 13
12 16
13 14
13 15
13 16
14 15
14 16
15 16
7
1 10
2 8
3 4 5 6
7 11 17
9
12
13 14 15 16
Hint
样例 1 解释
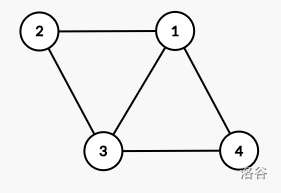
如图, 共有 ,, 三条路径,它们互相都没有相交的边。因此 与 在同一个边三连通分量中。
由于 , 点度都只有 ,不可能有三条边不相交的到其它点的路径,因此它们自己形成边三联通分量。
数据范围
- 对于 的数据,,。
- 对于 的数据,,。
- 对于 的数据,,。
- 对于 的数据,,。可能有重边和自环。

 京公网安备 11011102002149号
京公网安备 11011102002149号