题目背景

一九二九不出手，三九四九冰上走，五九六九隔河看杨柳；

七九河开，八九雁来，九九加一九，耕牛遍地走。

「九」自古以来就是一个奇妙的数字，而你今天要解决的问题，也与「九」有关。

题目描述

你有一个 $n$ 连环，和你熟知的九连环有着相同的结构。

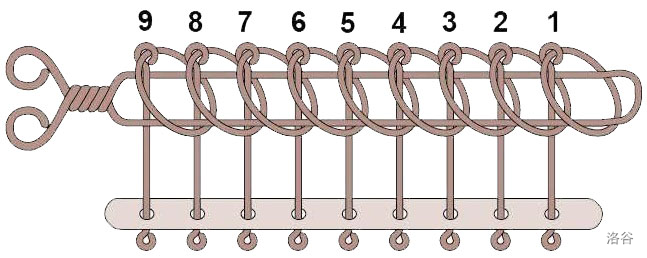
上图是一个九连环。

顾名思义，$n$ 连环有一个长长的横梁，上面挂着 $n$ 个 彼此影响 的环。

我们给这 $n$ 个环编号，其中最靠横梁头部的环为第 $1$ 个环，其次为第 $2$ 个环，以此类推……最靠横梁尾部的环为第 $n$ 个环；

定义 $f_i$ 表示第 $i$ 个环的状态，其中 $f_i = 1$ 表示这个环在横梁上，$f_i = 0$ 表示这个环不在横梁上；

定义 拆装一个环 为使环的状态 取反，即状态从 $1$ 变成 $0$ 或从 $0$ 变成 $1$。

这些环的合法拆装规则如下：

1. 第 $1$ 个环随时可以单独拆装；
2. 第 $k+1$ 个环可以单独拆装，当且仅当 $f_k=1$ 且 $\forall i < k$，都有 $f_i = 0$；
3. 若 $f_1 = f_2$，则第 $1,2$ 两个环可以一起拆装。

现在你需要解决的问题是：已知一个 $n$ 连环的初始状态，请你求出拆除这个 $n$ 连环的最少拆装步数。

输入格式

本题数据量较大，故采取 特殊 输入方式。

第一行一个正整数 $n$。

第二行一个正整数 $m$；

接下来 $m$ 行输入描述了初始状态：

第 $i + 2$ 行有两个整数 $len_{i}, st_{i}$，表示往初始的 $n$ 连环的尾部连续添加 $len_{i}$ 个状态为 $st_{i}$ 的环。

输出格式

一行共一个整数，表示从拆下这个 $n$ 连环所需要的最少拆装次数。

由于答案可能很大，你只需要输出答案对 $1201201201$ 取模后的结果。

4
3
1 1
1 0
2 1

7

15
4
5 1
2 1
4 0
4 1

15424

3
3
1 1
1 0
1 1

5

提示

本题采用 捆绑测试，开启 O2优化。

$\text{Subtask 1 (10 pts)}:$ 保证 $1 \le n \le 20$；

$\text{Subtask 2 (15 pts)}:$ 保证 $1 \le n\le 1000$；

$\text{Subtask 3 (15 pts)}:$ 保证初始状态中 只有 $1$ 个 $1$；

$\text{Subtask 4 (30 pts)}:$ 保证 $1 \le n \le 10^7$；

$\text{Subtask 5 (30 pts)}:$ 没有特殊限制。

对于所有数据，满足 $1 \le n \le 10^{18}$，$1 \le m \le 10^5$，$st_{i} \in \{0, 1\}$，$len_{i} \ge 1$

数据保证 $\sum\limits_{i=1}^m len_{i} = n$。

---

样例 #1 解释

样例描述的是 $4$ 连环，初始状态为 1101。

用最少合法拆装次数完成的方法如下：

1. 1101 -> 1100
2. 1100 -> 0100
3. 0100 -> 0111
4. 0111 -> 0110
5. 0110 -> 0010
6. 0010 -> 0011
7. 0011 -> 0000

共 $7$ 步。

---

题外话

本题中 $n$ 连环的第 $3$ 条拆装规则，在大部分的九连环玩法说明中都没有提到，但它确实是一个真实可行的操作呢！