Description

有 $n$ 个梦境场景，编号 $\in [1,n]$ 且互不相同。PF 有精神分裂症，他在同一时间会处于两个梦境。这两个梦境所在的场景编号差别的绝对值不能大于 $l$。场景之间有 $m$ 种单向关系，其中第 $i$ 个关系连接场景 $u_i$ 和 $v_i$。不存在不可能到达的场景。

每个场景都有一个快乐值，其中第 $j$ 个场景的快乐值为 $a_j$，在梦境第一次经过时增加。

一开始两个梦境均在场景 $1$，当两个梦境都移动到场景 $n$ 时，PF会醒来。

如果某次移动时，PF 目前梦境所在的两个场景 $A,B$ 都与某个场景 $C$ 直接相连，那么 PF 可以同时移动 两个梦境到达场景 $C$ 。否则，PF 一次只能移动一个梦境。

请你编一个程序，来计算醒来时可能得到的最大快乐值。

Input Format

第一行三个整数 $n,m,l$，分别表示场景的数量，场景之间的关系数量，以及 PF 两个场景距离的最大值。

接下来一行 $n$ 个整数，第 $i$ 个数表示编号为 $i$ 的场景的快乐值为 $a_i$，场景 $1$ 和场景 $n$ 的快乐值为 $0$。

接下来 $m$ 行，每行两个整数 $u,v(1\le u<v \le n)$，表示场景之间存在的一条单向关系。

Output Format

如果有解，一行一个整数 $q$，表示能获得的最大快乐值。

如果无解，只需输出 -1。

7 9 2
0 4 5 10 10 20 0
1 2
1 3
1 4
1 6
2 5
3 5
4 7
5 7
6 7

25

Hint

大样例

【样例解释 #1】

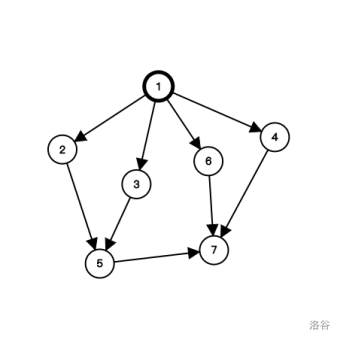
下文用 $A,B$ 表示目前正在进行的梦境：

移动梦境 $A \space 1 \to 3$，移动梦境 $B \space 1 \to 4$，移动梦境 $A \space 3 \to 5$，之后同时移动梦境 $A \space B$ 到达场景 $7$，快乐值总和为 $5+10+10 = 25$。

注意：如果想移动某一梦境到场景 $6$，那么另一梦境的编号必须大于等于 $4$。然而到 $6$ 的线路只有 $1\to 6$，而同时拥有场景 $1$ 和场景 $4$ 不满足中间相隔场景 $\le l$，故唯一通过场景 $6$ 的方案为将两个梦境同时移动到场景 $6$，而这么做能得到的快乐值为 $20$。

【数据范围与约定】 | 测试点编号 | $n \le$ | $m \le$ | $l \le$ | $a_i \le$| 时间 | 特殊性质 | | :----------: | :----------: | :----------: | :----------: |:----------: | :----------: |:----------: | | $1,2$ | $10$ | $15$| $5$ | $50$ | $1\text s$ |无 | | $3\sim 4$ | $16$ | $40$ | $8$ | $5 \times 10^3$ |$1\text s$ |无 | | $5\sim 6$ | $16$ | $120$ | $8$ | $5 \times 10^3$ |$1\text s$ |无 | | $7 \sim 10$ | $100$| $10^3$|$10$ | $10^4$|$1 \text s$ |无| | $11$ | $100$| $10^3$|$10$ | $10^4$|$1\text s$ |场景是一棵树| | $12 \sim 14$ | $10^3$| $10^4$|$10$ | $10^4$|$1\text s$ |无| | $15,16$ | $5\times10^3$| $3\times10^4$|$10$ | $10^4$|$1\text s$ |无| | $17,18$ | $5\times10^3$| $3\times10^4$|$11$ | $10^4$|$2\text s$ |无| | $19,20$ | $5\times10^3$| $3\times10^4$|$12$ | $10^4$|$3\text s$ |无|

对于 $100\%$ 的数据，$1\le u<v \le n$, $1 \le n \le 5\times 10^3$, $1 \le m \le 3\times 10^4$, $1 \le a_i \le 10^4$, $1 \le l \le 12$。

输入保证每个场景都能从起点到达，并且都能连到终点。

输入不保证没有重边。

输入不对 $u,v$ 的编号差做任何保证。

【移动范例】

假设 $l=2$ 且关系存在，下面的格式表示 $A \space B$ $\to$ $A' \space B'$ 一次移动：

• $1 \space 3 \to 5\space 3$ (√)
• $1 \space 3 \to 1\space 4$ (×)
• $1 \space 3 \to 8\space 8$ (√)
• $1 \space 3 \to 6\space 8$ (×)