Description

这个游戏是在一个有向图（不保证无环）上进行的。每轮游戏开始前，她们先在图上选定一个起点和一个终点，并在起点处放上一枚棋子。

然后两人轮流移动棋子，每次可以将棋子按照有向图的方向移动至相邻的点。

如果谁先将棋子移动至终点，那么谁就胜利了。同样，如果谁无法移动了，那么谁就失败了。

两人轮流操作，请问，他们是否有必胜策略呢？

答案为一个整数 0 或 1 或 -1，其中 1 表示（先手）有必胜策略，-1 表示后手有必胜策略，0 表示两人均无必胜策略。

Input Format

第$\text{1}$行有三个整数 $n,m,q$ ，表示图上有 $n$ 个点， $m$ 条边，一共进行 $q$ 轮游戏。
接下来 $m$ 行，每行输入两个数 $u_i,v_i$ ，表示 $u_i$ 到 $v_i$ 有一条边。
接下来 $q$ 行，每行两个数 $x,y$ ，表示每轮操作的起点和终点。数据保证起点，终点不同

Output Format

对于每轮游戏，仅输出一个整数 0 或 1 或 -1，其中 1 表示先手有必胜策略，-1 表示后手有必胜策略，0 表示两人均无必胜策略。

7 7 1
1 2
2 3
3 4
4 5
3 6
7 5
6 7
1 5

1

5 5 2
1 2
2 3
3 1
3 4
4 5
1 5
4 3

0
1

Hint

样例解释 #1

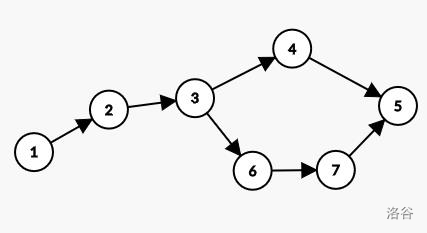
为描述题意，假设两人为 A（先手）和 B

如图，A 先走，走到 $2$，B 走到 $3$，接下去 A 可以选择走到 $4$ 或 $6$，若走到 $4$，接下去 B 可以走到终点，故不可取。若选择走到 $6$，那么 B 只能走到 $7$，A 可以走到终点。所以 A 有必胜策略。

样例解释 #2

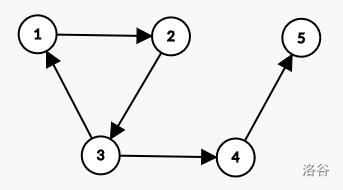
如图，起点为 $1$，终点为 $5$ 时， A 和 B 会沿着 $1-2-3-1$ 的顺序轮流走。因为如果谁先走到 $4$，那么下一个人就可以走到终点。故谁都没有必胜策略。

起点为 $4$，终点为 $3$ 时，A 先走到 $5$，B 无路可走，故 B 失败。

数据范围

对于 $10\%$ 的数据，保证图是一条链。

对于 $50\%$ 的数据，$1\leq n\leq 10^3$，$1\leq m\leq 2\times10^3$，$1\leq q\leq 10$。

对于 $70\%$ 的数据，$1\leq n\leq 10^5$，$1\leq m\leq 2\times10^5$，$1\leq q\leq 10$。

对于 $100\%$ 的数据，$1\leq n\leq 10^5$，$1\leq m\leq 5\times10^5$，$1\leq q\leq 500$。