Description

请注意，本题的时间限制为 5s！

探险家小 A 和小 B 需要用灯泡照亮这个森林。

有 $n$ 个灯泡，编号为 $1, 2, \cdots, n$。小 A 用 $n - 1$ 条红色绳子把它们连成了一棵树，小 B 用 $n - 1$ 条蓝色绳子把它们连成了另一棵树。

一开始所有灯泡都是熄灭的，现在要点亮若干个灯泡。小 A 喜欢联通块，而小 B 喜欢链。他们想知道：有多少种点亮灯泡的方案，满足点亮的灯泡在小 A 的树上形成一个联通块，在小 B 的树上形成一条链呢？

Input Format

第一行一个数 $T$，表示有 $T$ 组数据，对于每组数据：

第一行一个数 $n$。

第 $2$ 行到第 $n$ 行，第 $i + 1$ 行两个数 $a_i, b_i$，表示小 A 的树上的一条边。

第 $n + 1$ 行到第 $2n - 1$ 行，第 $i + n$ 行两个数 $c_i, d_i$，表示小 B 的树上的一条边。

Output Format

输出 $T$ 行，第 $i$ 行是第 $i$ 组数据的答案。

3
3
1 2
2 3
1 2
1 3
5
1 2
1 3
2 4
2 5
1 2
2 3
3 4
4 5
5
3 1
3 2
3 4
3 5 
1 2
2 3
3 4
3 5

5
9
14

Hint

样例解释：

三组数据的图解：

样例 1：

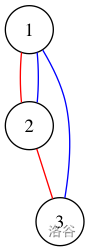
样例 2：

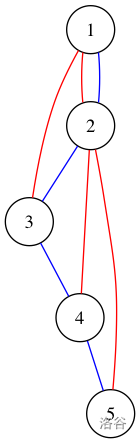
样例 3：

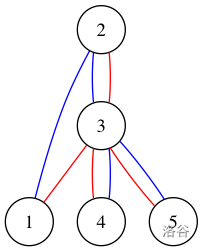
对于第一组数据，可以点亮的灯泡集合有：

• $\{1\}$；
• $\{2\}$；
• $\{3\}$；
• $\{1, 2\}$；
• $\{1, 2, 3\}$。

注意不能点亮集合 $\{1, 3\}$，因为编号为 $1, 3$ 的灯泡在小 A 的树上不构成联通块；也不能点亮集合 $\{2, 3\}$，因为编号为 $2, 3$ 的灯泡在小 B 的树上不构成一条链。

对于第二组数据，可以点亮的，至少包含两个灯泡的的灯泡集合有：

• $\{1, 2\}$；
• $\{1, 2, 3\}$；
• $\{1, 2, 3, 4\}$；
• $\{1, 2, 3, 4, 5\}$。

显然大小为 $1$ 的灯泡集合都合法，所以答案为 $4 + 5 = 9$。

限制与约定：

对于 $20 \%$ 的数据，$n \le 50$，满足特殊限制 $X$。
对于 $40 \%$ 的数据，$n \le 3000$，满足特殊限制 $X$。
对于 $70 \%$ 的数据，满足特殊限制 $X$。
对于 $100 \%$ 的数据，$T = 3, 1 \le n \le 10^5$。

特殊限制 $X$：$c_i = i, d_i = i + 1$，也就是说小 B 的树是一条链，编号相邻的点之间有边。