#P6513. [QkOI#R1] Quark and Tree
[QkOI#R1] Quark and Tree
Description
给定一棵包含 个节点的树,每个节点上有一个点权,点的编号为 ,请加一条不存在于给定的树中的边(且不能为自环),使加边后得到的基环树上所有点的深度与该点点权乘积之和最大。
我们认为基环树上的点的深度指该节点到环上的最短距离,特别地,环上的节点深度为 。
形式化地,你需要添加一条不存在于给定的树中的边(且不能为自环),并最大化:
其中 为节点 的权值, 为节点 在基环树中的深度。
Input Format
第一行包含一个整数 ,表示树中点的个数。
第二行包含 个整数,第 个整数表示节点 的点权 。
接下来 行,一行两个整数 ,表示 和 在树中有一条边连接。
Output Format
输出包含一行一个整数,表示加边后生成的基环树中,各个节点的深度与其点权乘积之和的最大值。
7
1 1 1 1 1 1 1
1 2
1 3
2 5
3 4
3 7
4 6
8
5
-6 3 -1 -7 -2
1 2
1 3
3 4
5 1
3
Hint
样例解释
样例 1 给出的树如下图所示:
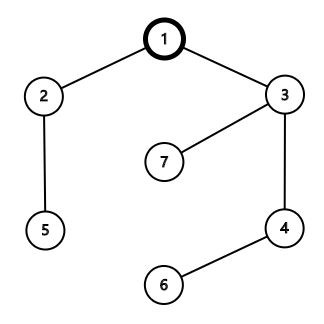
可以添加边 ,则新生成的基环树如下图所示:
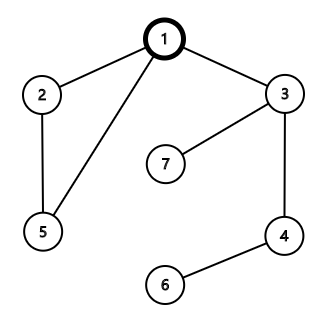
各节点深度见下表:

数据范围
本题采用捆绑测试。
对于所有数据,,,。
- 子任务 ( 分):。
- 子任务 ( 分):。
- 子任务 ( 分):。
- 子任务 ( 分):无特殊限制。

 京公网安备 11011102002149号
京公网安备 11011102002149号