题目描述

有如下七种俄罗斯方块的图形：

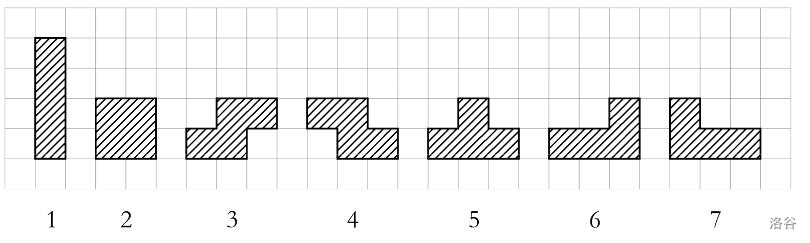
在使用时可以将它们旋转 $90$，$180$，$270$ 度或不进行旋转。

现在有一个有 $n$ 列，高度不限的方格阵，第 $i$ 列的底部 $a_i$ 行已经有了图形（即最下方 $a_i$ 行在之前已经被放上了方块），每一列只有底部的连续若干行有方块。

下一次要落下的方块是 $m$ 号方块，请求出下落后有多少种布局满足不存在任何一个格子，它本身不被方块占据但是上方的格子被方块占据。也即求出多少种布局满足任何一列只有底部连续若干行有方块。

两种布局不同当且仅当存在一个格子，在其中一种布局中该格子被方块占据，在另一种布局中不被占据。

输入格式

第一行有两个整数，分别表示方格阵的行数 $n$ 和下一次下落的方块编号 $m$。

第二行有 $n$ 个整数，第 $i$ 个整数 $a_i$ 表示第 $i$ 列的只有底部连续 $a_i$ 行有方块。

输出格式

输出一行一个整数表示答案。

6 5
2 1 1 1 0 1

5

5 1
0 0 0 0 0

7

9 4
4 3 5 4 6 5 7 6 6

1

提示

样例 1 解释

下面六张图中，左上角的图是方格阵的初始布局，另外五张图是五种情况。

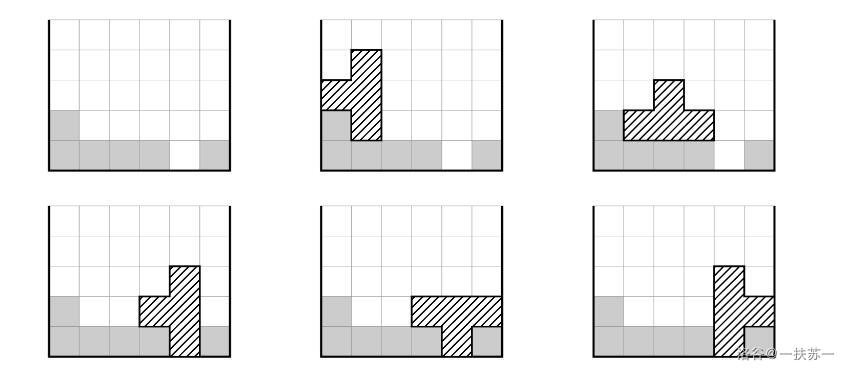
数据规模与约定

对于全部的测试点，保证：

• $1 \leq n \leq 100$，$1 \leq m \leq 7$。
• $0 \leq a_i \leq 100$。

说明

题目译自 COCI2006-2007 Regional Competition T2 TETRIS，翻译来自 @一扶苏一。