#P6455. 不可视境界线[环版本]
不可视境界线[环版本]
Description
有 个半径为 的圆,画在一个长度为 的首尾相接的纸环上。
所有的圆心都在同一高度,可以看做在纸上画一个数轴然后卷起来,圆心的位置用这个数轴上的点描述。
如果无法理解纸环上圆的分布,可以查看样例解释以及子问题。
要求选出 个圆,使得所有圆的并面积最大。
注意,您需要回答确切的选取方案而不是仅仅给出最大并面积。
Input Format
第一行包含四个整数 ,意义如题目所述。
第二行包含 个整数,第 个整数 描述了第 个圆心在纸环上的位置(数轴上的坐标)。
对于 ,有 。
Output Format
一行包含 个整数,分别表示您选取的圆的编号,由SPJ来计算并面积。
您需要保证这些编号严格递增,并且在 以内,否则被认为不合法而不得分。
与标准答案相对误差不超过 ,且绝对误差不超过 则认为正确。
通过估算,答案不会超过 量级。
5 3 10 30
0 7 14 21 28
2 3 5
10 3 10 65
0 7 15 24 30 36 41 49 57 63
3 6 9
30 10 50 169
0 7 14 21 28 35 42 45 51 55 61 65 68 75 79 83 87 94 97 105 113 118 126 133 140 147 151 156 163 167
3 5 8 11 15 19 21 24 27 30
Hint
样例解释 :
- 样例1 : 最终的并面积约为 。
圆的分布如图所示,其中, 和 是同一个圆, 和 是同一个圆。
可以视作向右平移 个单位长度而得,事实上就相当于在纸环上绕了一圈回到起点。
由于是同一个圆,被红色部分覆盖的面积不能重复计算,最大的并面积即为蓝色部分的面积。
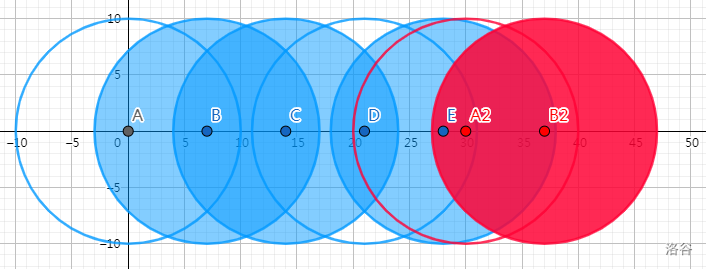
-
样例2 : 最终的并面积约为 。
-
样例3 : 最终的并面积约为 。
数据范围与约定 :
| 子任务编号 | n | k | 时限 |
|---|---|---|---|
| 1 | - | ||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | - |
时限在 std 耗时的两倍以上。
对于所有的数据, ,,,,。
表格中均为上界。注意,一些下界限制可能帮助省去了问题的某些边界情况。

 京公网安备 11011102002149号
京公网安备 11011102002149号