#P6407. [SDOI2012] 棋盘覆盖
[SDOI2012] 棋盘覆盖
Description
在一个 的棋盘内,有 个方格被称为特殊方格。我们要使用一组俄罗斯方块来覆盖这个棋盘,保证特殊方格不能被覆盖,非特殊方格只能被一个俄罗斯方块覆盖,求最多能容纳的俄罗斯方块的数量。
已知有以下三组俄罗斯方块,一个棋盘可能用其中的某一组。
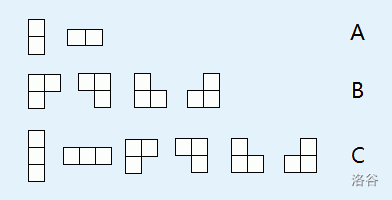
Input Format
第一行三个整数 和一个字符 type 为所用的俄罗斯方块组。
接下来 行每行两个整数 表示第 行第 列为特殊方格。
Output Format
一个整数,为所求的答案。
8 8 0 A
32
7 6 6 C
3 1
3 6
5 3
5 4
5 7
6 7
12
Hint
对于测试点 ,,,type 为 A;
对于测试点 ,, 为 的整数次幂,,type 为 B;
对于测试点 ,,,type 为 C。

 京公网安备 11011102002149号
京公网安备 11011102002149号