#P6310. 「Wdsr-1」仓库建设
「Wdsr-1」仓库建设
Description
因为幻想乡倡导“幻想乡命运共同体”意识,河童们决定帮助人类修建一些粮仓防止饥荒再次发生。
人间之里有 座城市和 条双向道路,第 条道路连接 两座城市,长度为 个单位。
由于每座城市的科技水平不同,从不同城市出发的运粮车的储油量不同。第 座城市的运粮车的储油量只能支持运粮车行驶 个单位。当然,城市与城市之间是友好的,无论到达哪个城市,热心的当地民众都会给运粮车加满油。
河童科技高度发达,所以仓库容纳的粮食可以视作无限。只有粮仓能发出运粮车。
现在要选择一些城市建设仓库,使得每一个城市都可以从粮仓中得到粮食。为了节约资源,河童希望仓库的数量最小。
但妖怪有时会占据一个城市,所以需要算出在任意一个城市不能建设粮仓时需要的最小粮仓数。
Input Format
第一行两个整数 ,意义如题面所述。
接下来 行每行 3 个整数 ,意义如题面所述。
接下来一行 个整数 ,意义如题面所述。
Output Format
输出一行 个整数。
第一个整数表示最少需要多少粮仓;接下来 个整数,第 个整数表示 号城市不能建粮仓所需的最小的粮仓数。
如果第 个城市不能建粮仓时,其他城市建粮仓不能到达这个城市,则输出 -1。
4 4
1 2 2
1 3 3
2 4 1
3 4 4
2 1 3 2
1 1 1 -1 1
Hint
样例解释
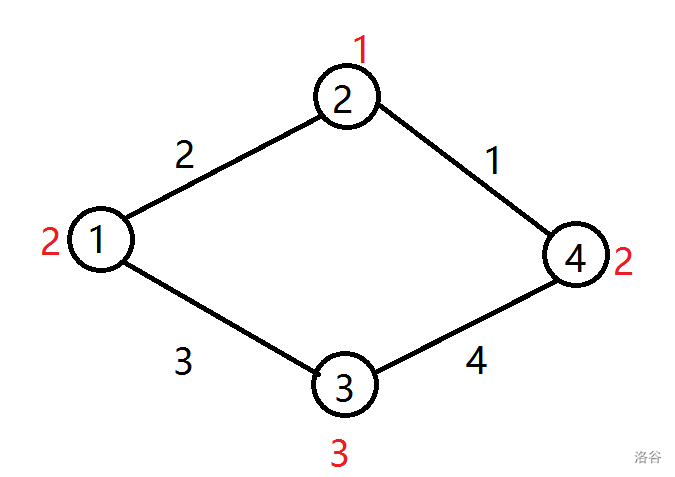
这是样例画出来的图,显然在 3 号城市建立粮仓就可以解决问题,当 3 号城市不能建粮仓时,其他的城市无论怎么建粮仓,粮食也运不到 3 号城市,输出 -1。
数据范围
对于 的数据,保证 。
对于另外 的数据,保证 。
对于 的数据,保证 $1\le n,m \le 3\times 10^5,1\le u_i,v_i\le n,1\le w_i,x_i\le 10^6$,保证图联通。

 京公网安备 11011102002149号
京公网安备 11011102002149号