#P6291. [eJOI 2017] 骆驼
[eJOI 2017] 骆驼
Description
我们在棋盘上引入一个新的棋子,称之为“骆驼棋”。棋子跳跃规则:你可以将它移动到水平或垂直方向上的一个位置,使得新位置与旧位置之间隔着 格;或者像四个斜对角线的方向之一移动,使得新位置与旧位置之间恰好相隔一个格子。如图,棋盘的中心就是棋子的位置, 个打上 ”“标记的就是可以移动到的位置。显然,棋子不可以跳出棋盘。
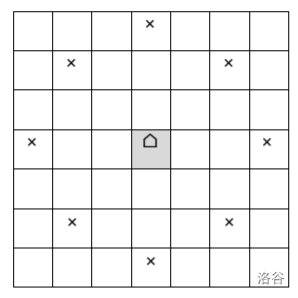
整个棋盘是 行 列的,其中保证 。
一开始,棋子在棋盘的左上角。经过一系列移动,使得整个棋盘每一个格子都被走过恰好一次,并且最后的位置与开始位置之间恰好可以以骆驼棋一步互相到达,这就是所谓的”骆驼循环“。
你需要写一个程序,找到给定棋盘的”骆驼循环”。或者判断是否存在“骆驼循环”。
Input Format
输入仅一行,一个正整数 。
Output Format
首先,如果不存在输出 NO。
输出包含一个 的方阵。
方阵包含 个不同的正整数,大小在 范围内,表示每一个格子的访问顺序。那么第一个数字就是 。
例如,第 行第 列的数为 说明这一个位置的格子是第 个被走到的。详见样例。
10
1 52 29 8 51 28 9 50 37 16
85 95 59 86 94 66 87 93 65 88
40 19 100 39 18 76 38 17 77 49
2 53 30 7 58 27 10 89 36 15
84 96 60 75 99 67 72 92 64 71
41 20 82 44 23 90 45 24 78 48
3 54 31 6 57 26 11 68 35 14
83 97 61 74 98 62 73 91 63 70
42 21 81 43 22 80 46 25 79 47
4 55 32 5 56 33 12 69 34 13
Hint
Special Judge 计分标准
如果可行解有多个,输出任意一个就可以拿到这个测试点的分数。
如果输出不完全或发现不正确的情况你可能会得到一个 UKE。
如果在不该输出 NO 的地方输出了 NO ,你们你会得到 WA,以及一句 wrong output format Expected integer, but "NO" found
输入输出样例解释
棋子移动的方式为:(表示第一行第一列) $\rightarrow (4,1) \rightarrow (7,1) \rightarrow \text{etc.}$
最后棋子在 处停止,恰好可以一步走到起点。
附图:
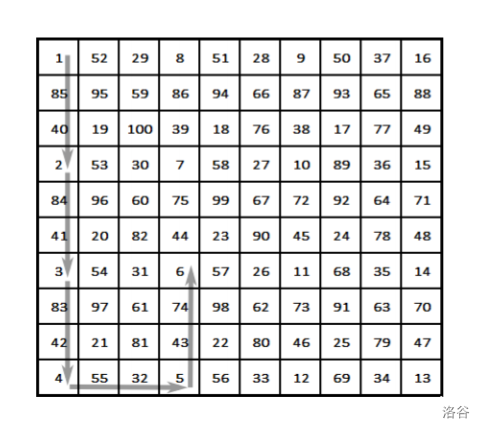
数据规模与约定
对于所有数据,保证 ,且 是 的倍数。
本题共 个测试点。
- 对于其中一个测试点,有 ,单点分值比例为 。
- 对于其他 个测试点,无其他限制,单点分值比例为 。
说明
翻译提供:@_Wallace_

 京公网安备 11011102002149号
京公网安备 11011102002149号