#P6235. [eJOI 2019] 矩形染色
[eJOI 2019] 矩形染色
Description
Srečko 想给一个 行(从 至 编号) 列(从 至 编号)的的矩形网格的每一个格子染上色。一开始,整个矩形都是白色的。每一步,他都会选择一条对角线,并给这条对角线上的所有格子染上色。每个对角线染色都需要一定的费用(忽略长度),这就导致某些对角线的染色费用有高于其他某些对角线。
你需要写一个程序,读入各个对角线的染色费用,求出将所有格子染上色的最小总费用。
注意,同一个格子被重复多次地染色是被允许的。
一个 行 列的矩形网格共有 。
例:当 时,共有 条对角线:
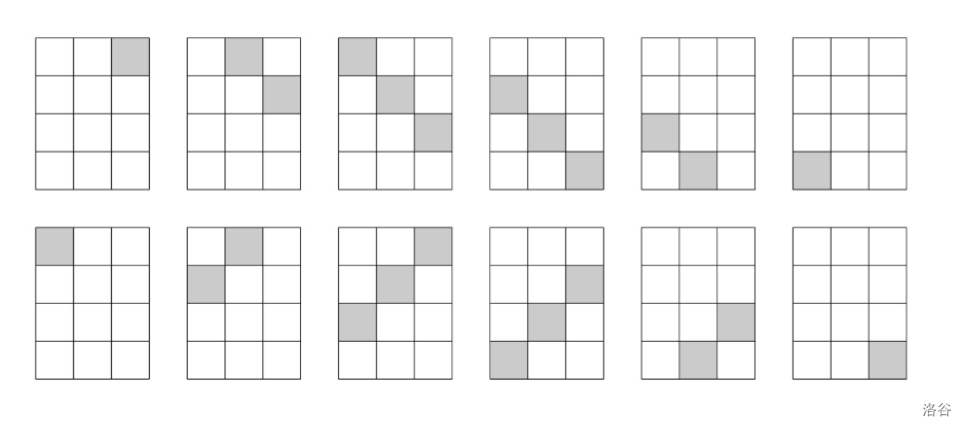
Input Format
输入共 行。
第一行:两个整数 ;
第二行:共 个整数,描述所有 方向的对角线。第 个整数表示 这个单个的格子,第 个整数表示 两个格子,以此类推。
第三行:共 个整数,描述所有 方向的对角线。第 个整数表示 这个单个的格子,第 个整数表示 两个格子,以此类推。
Output Format
一个整数表示答案。
2 2
1 3 1
1 3 1
4
4 3
2 3 9 3 4 3
2 3 3 1 2 4
14
Hint
【输入输出样例解释】
样例 1 解释
- 在这个情况中,如下的方案可以得到最小花费:
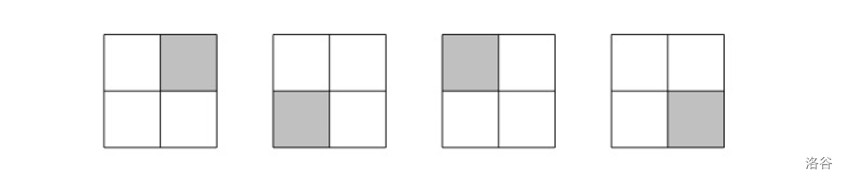
总花费 。
样例 2 解释
- 对于这个情况,如下的方案可以使花费最小化:
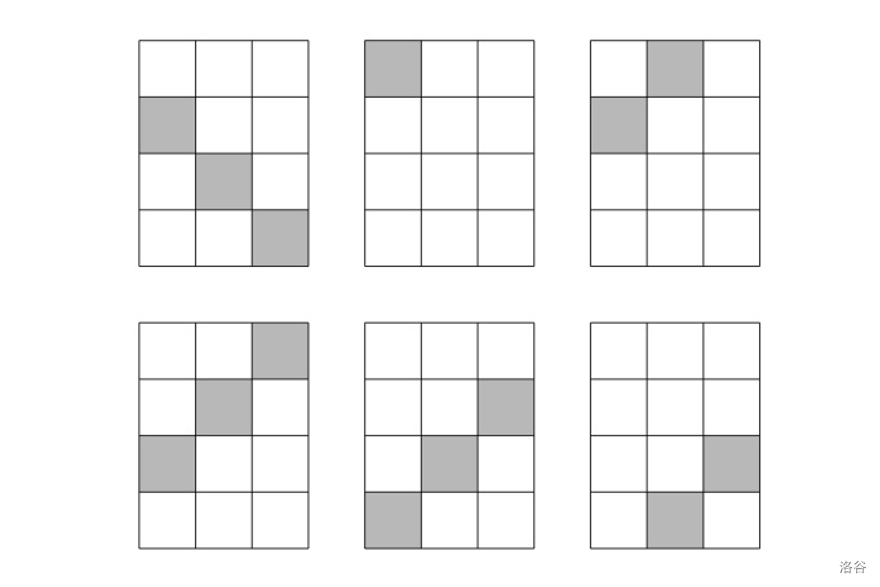
总花费 。
【数据规模与约定】
本题采用多测试点捆绑测试,共有 7 个子任务。
- Subtask 1(10 points):
- Subtask 2(10 points):
- Subtask 3(10 points):
- Subtask 4(20 points):
- Subtask 5(10 points):
- Subtask 6(20 points):
- Subtask 7(20 points):无其他限制。
对于所有数据,保证 ,每条对角线的染色费用
【说明】
原题来自:eJOI2019 Problem E. Colouring a rectangle。
翻译提供:@_Wallace_。

 京公网安备 11011102002149号
京公网安备 11011102002149号