#P6234. [eJOI 2019] T形覆盖
[eJOI 2019] T形覆盖
Description
如果你玩过俄罗斯方块,应该见过如下图形:
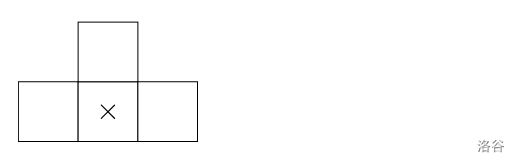
我们称它为一个 T 形四格拼板 。其 中心 被标记为 。
Manca 画了一个 行 列的长方形网格。行从 至 编号,列从 至 编号。她将网格中的一些格子标记为 特殊格子 。然后,她想要她的朋友 Nika 帮助她将 T 形四格拼板按找如下规则摆放:
- 特殊格子的数量与 T 形四格拼板的数量相同,每个 T 形四格拼板的中心在网格上的位置必须是特殊格子。
- T 形四格拼板之间不能有重叠部分。
- 所有拼板的部分均在网格内。
注意,T 形四格拼板有四种摆放方式:。
如果方案不存在,输出 No,否则请找出一种方案使得被拼板覆盖的数总和最大,求出这个最大值。
Input Format
第一行两个整数 分别表示行数和列数。
接下来 行,每行 个整数,第 行第 个数(从 开始编号)表示方格中第 行第 列的数 。
接下来一行,一个整数 ,表示特殊格子的数量。
接下来 行,每行两个整数 ,表示第 个被标记的特殊格子的位置。
Output Format
如果有方案,输出可能的被覆盖的格子内数总和的最大值,否则输出 No。
5 6
7 3 8 1 0 9
4 6 2 5 8 3
1 9 7 3 9 5
2 6 8 4 5 7
3 8 2 7 3 6
3
1 1
2 2
3 4
67
5 6
7 3 8 1 0 9
4 6 2 5 8 3
1 9 7 3 9 5
2 6 8 4 5 7
3 8 2 7 3 6
3
1 1
2 2
3 3
No
Hint
输入输出样例 1 解释
其中一种最优的方案如下:
- 位置的摆放方式为 。
- 位置的摆放方式为 。
- 位置的摆放方式为 。
数据规模与约定
本题采用多测试点捆绑测试,共有 7 个子任务。
- Subtask 1(5 points):,保证对于所有 ,。
- Subtask 2(10 points):,保证对于所有 ,若 ,则 与 有邻边。
- Subtask 3(10 points):,保证对于所有 ,。
- Subtask 4(10 points):所有特殊格子在同一行。
- Subtask 5(15 points):。
- Subtask 6(20 points):
- Subtask 7(30 points):无其他限制。
对于所有数据,满足:$1\le k\le nm\le 10^6,a_{ij}\in[0,10^3],r_i\in[0,m),c_i\in[0,n)$。
说明
原题来自:eJOI2019 Problem C. T - Covering。
翻译来自:LibreOJ。

 京公网安备 11011102002149号
京公网安备 11011102002149号