边权树的路径xor可以通过树上前缀和变成点权树的两点xor 我们可以发现问题即找出一个点i使得i子树内选两个点的xor加上i的子树外选两个点的xor最大 发现每个点的子树外选两个点最大xor和是可以用上一个题的做法O(nlogn)算出来的，问题在于子树内如果需要计算每个点的答案的话是O(nlog^2n)的 先把每个点子树外的答案算出来，即为f[i] 还是找出全局最大的x xor y 1.x和y都在i子树内，这种情况i一定是lca(x,y)的祖先，求这条路径上最大的f[i]即可 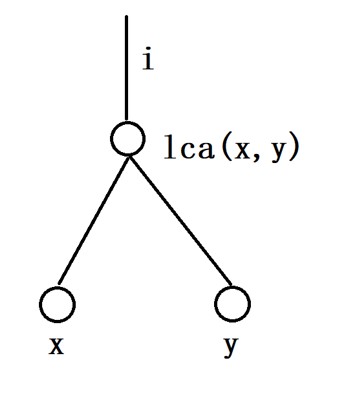3.x在子树内y在子树外，以及对称的情况 这种情况我们从x扫到lca(x,y)算一遍子树内最大xor和，从y扫到lca(x,y)算一遍子树内最大xor和即可 这里插入次数也是O(n)的

总时间复杂度O(nlogn)