题目描述

Shik 大佬发明了一种游戏。这种游戏在 $N \times N$ （$N$ 为偶数）的网格上进行，如图所示（左上角为 $(1,1)$，右下角为 $(N,N)$）：

这种游戏的规则如下：

• 初始局面为：在最左边一列和最右边一列的网格上分别放置着红方和蓝方的棋子，在最上面一行左半部分和最下面一行左半部分也放置着红方的棋子，在最上面一行右半部分和最下面一行右半部分也放置着蓝方的棋子；
• 红方先走，蓝方后走；
• 有一方只剩下 $N\div 2$ 颗棋子时，游戏结束，另一方获胜；
• 有一方无棋可走时，游戏结束，另一方获胜；
• 每次走棋可以让一颗棋子往上下左右方向移动 $1$ 格，但目标格上不能有棋子；
• 同时满足以下条件时可以吃掉对方棋子：在一行（或一列上），有且仅有 $N-1$ 颗棋子（当 $N>4$ 时为 $N-2$ 颗也可），其中有 $N-2$ 颗己方棋子（当 $N>4$ 时为 $N-3$ 颗也可），另外 $1$ （当 $N>4$ 时为 $2$ 颗也可）颗棋子为敌方的，我方的棋子全部相邻，敌方棋子全部相邻，并且我方有一颗棋子与敌方相邻，而且此局面为我方主动走成，则我方可以把这一列上敌方的棋子全部吃掉。

现在，请你模拟走棋的过程。

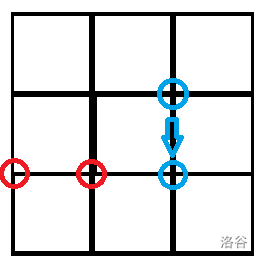
以上为一个不可以吃子的局面。（红吃蓝）

但假如蓝棋本来就在 $(3,3)$，红棋从 $(2,2)$ 走到 $(2,3)$，就可以吃子。

若不能理解，强烈建议手推一遍样例。

输入格式

输入文件的第一行有两个整数 $N$ 和 $K$，表示棋盘的大小和走棋的总步数。

接下来 $K$ 行，每行四个整数 $a,b,c,d$，表示某一方的原本在 $(a,b)$ 的棋子走到了 $(c,d)$。从第二行开始算起，第偶数行表示蓝方，第奇数行表示红方。

输出格式

分三种情况输出答案：

• 数据不合法：输出 $0$。
• 这一局还没有结束：第一行输出 $1$，接下来 $N$ 行，每行 $N$ 个字符，表示目前的局面状态。用h表示红方棋子，l表示蓝方棋子，.表示此网格为空。若此局面某一方可以吃子，输出吃子后的状态。
• 这一局已经结束：第一行输出 $2$，第二行输出red或blue，表示哪一方获胜。第三行至第 $N+2$ 行，输出获胜时的局面。用h表示红方棋子，l表示蓝方棋子，.表示此网格为空。若此局面某一方可以吃子，输出吃子后的状态。你的程序应该忽略使你判断出胜负那一行之后的所有输入。

4 1
1 4 1 3

0

4 2
1 3 2 3
3 4 3 3

1
hhll
h..l
..ll
hh.l

6 7
1 3 2 3
4 1 4 2
3 1 4 1
6 4 5 4
2 1 3 1
5 4 6 4
1 1 2 1

1
.hhh..
h..l.l
.h...l
h....l
h....l
hhhlll

6 22
1 3 2 3
4 1 4 2
3 1 4 1
6 4 5 4
2 1 3 1
5 4 6 4
1 1 2 1
6 2 5 2
3 1 3 2
6 4 5 4
2 1 2 2
4 6 4 5
3 6 4 6
5 4 6 4
2 6 3 6
6 4 5 4
1 6 2 6
6 5 6 6
2 6 2 5
6 6 5 6
2 5 2 6
6 6 5 6

2
red
...h..
hhh...
.h...l
h...l.
h..l..
.hhh..

提示

样例 4 说明：第 21 歩时，红方已胜，因此第 22 歩的非法移动应该忽略。

对于 $30\%$ 的数据，不存在吃子的情况；

对于 $60\%$ 的数据，$N=4$；

对于 $80\%$ 的数据，$4\le N\le 6$；

对于 $100\%$ 的数据，$4\le N\le 10$，$1 \le K \le 10^3$。