#P5983. [PA 2019] Osady i warownie 2
[PA 2019] Osady i warownie 2
Description
的网格,从上到下依次为第 到 行,从左到右依次为第 到 列,每个点都不是障碍格。
定义一条从起点 到终点 的路径是合法的,当且仅当这条路径经过恰好 个格子(包括起点和终点),且每一步要么往右走一格,要么往下走一格。当然,这条路径不能经过障碍格(包括起点和终点)。
你有一个 变量 ,你现在需要模拟 次操作,每次操作会给出三个非负整数 ,令 $x=(r \operatorname{xor} v)\bmod n,y=(c \operatorname{xor} v)\bmod m$:
- 如果 是障碍格,那么忽略这次操作,输出
NIE。 - 否则如果将 变成障碍格后仍然存在合法路径,那么将 变成障碍格,输出
NIE。 - 否则如果将 变成障碍格后不存在合法路径,那么输出
TAK,并将 修改为 。
Input Format
第一行三个正整数 。
接下来 行,每行三个非负整数 。
Output Format
对于每个操作输出一行 TAK 或 NIE。
3 5 7
0 1 123
1 0 0
4 8 0
2 2 16
2 3 0
18 19 17
3 0 0
NIE
TAK
NIE
TAK
NIE
TAK
NIE
Hint
对于 的数据,, ,。
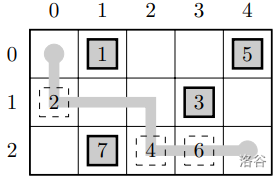
解释:

 京公网安备 11011102002149号
京公网安备 11011102002149号