题目描述

有一块 $n\times m$ 的矩形巧克力，准备将它切成 $n\times m$ 块。

巧克力上共有 $n-1$ 条横线和 $m-1$ 条竖线，你每次可以沿着其中的一条横线或竖线将巧克力切开，无论切割的长短，沿着每条横线切一次的代价依次为 $y_1,y_2,…,y_{n-1}$，而沿竖线切割的代价依次为 $x_1,x_2,…,x_{m-1}$。

例如，对于下图 $6\times4$的巧克力：

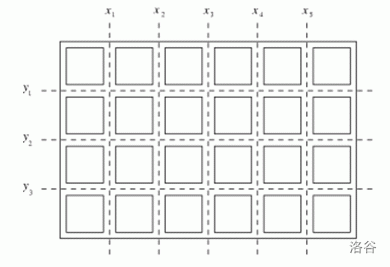
我们先沿着三条横线切割，需要 $3$ 刀，得到 $4$ 条巧克力，然后再将这 $4$ 条巧克力沿竖线切割，每条都需要 $5$ 刀，则最终所花费的代价为 $y_1+y_2+y_3+4\times (x_1+x_2+x_3+x_4+x_5)$。

当然，上述简单切法不见得是最优切法，那么怎样切割该块巧克力，花费的代价最少呢？

输入格式

第一行为两个整数 $n$ 和 $m$。

接下来 $n-1$ 行，每行一个整数，分别代表 $x_1,x_2,…,x_{n-1}$。

接下来 $m-1$ 行，每行一个整数，分别代表 $y_1,y_2,…,y_{m-1}$。

输出格式

输出一整数，为切割巧克力的最小代价。

6 4
2
1
3
1
4
4
1
2

42

提示

对于 $100\%$ 的数据，$1\le n\le 10000$，$1\le m\le 10000$。