题目背景

小 $\mathrm{A}$ 在学物理。

老师在讲“平面镜成像”这个物理现象。

但老师讲课太无聊，所以他就睡着了。

题目描述

小 $\mathrm{A}$ 梦见自己站在了一个平台上，在他的周围有一些平面镜，我们假定他的位置为 $(0,0)$。

他发现，每个平面镜都有一个初始不透明度，记做 $v_i$。

下文中，我们定义：

• 一个射线的“不透明度”为：该射线穿过的所有平面镜的初始不透明度之和。

• 一个平面镜的“视觉不透明度”为：所有从 $(0,0)$ 发出且经过该平面镜的射线的不透明度最大值。

小 $\mathrm{A}$ 突然发现自己能够控制这些平面镜，于是就有了下面这道题目。

小 $\mathrm{A}$ 需要你完成以下操作：

1 x1 y1 x2 y2 v：变出一个两端分别在 $(x_1,y_1),(x_2,y_2)$，初始不透明度为 $v$ 的平面镜。

2 d：摧毁第 $d$ 个变出来的平面镜，保证未被摧毁。

3 x y：设 $\mathrm{A=(0,0),B=(x,y)}$，询问射线 $\mathrm{AB}$ 的不透明度。

4 d：询问第 $d$ 个平面镜的视觉不透明度，如已被摧毁则输出 oops!。

输入格式

第一行，一个整数 $n$，表示操作次数。

接下来 $n$ 行，第 $i$ 行先是一个整数 $opt$，然后：

• 如果 $opt=1$，五个整数 $x_1,y_1,x_2,y_2,v$。

• 如果 $opt=3$，两个整数 $x,y$。

• 否则一个整数 $d$。

输出格式

对于每一个 $3,4$ 询问，输出一行答案。

11
1 -1 2 2 -1 7
1 2 2 -1 0 10
1 2 1 1 -1 17
3 5 4
3 -99999 0
3 -3 6
3 1 -1
4 2
2 1
4 2
4 1

7
10
17
17
17
10
oops!

提示

---

样例解释

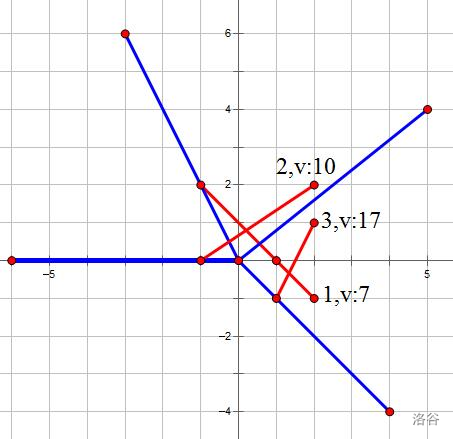
如图，蓝色代表射线，红色代表平面镜。

对于第 $1$ 次询问：可以看出射线只穿过了平面镜 $1$，答案为 $7$。

对于第 $2$ 次询问：可以看出射线只穿过了平面镜 $2$，答案为 $10$。

对于第 $3$ 次询问：可以看出射线穿过了平面镜 $1,2$，答案为 $7+10=17$。

对于第 $4$ 次询问，可以看出射线穿过了平面镜 $3$，答案为 $17$。

对于第 $5$ 次询问，可以看出穿过平面镜 $2$ 的不透明度最大的射线为 $(0,0)(2,2)$（射线不唯一），穿过了平面镜 $1,2$，答案为 $7+10=17$。

对于第 $6$ 次询问，可以看出穿过平面镜 $2$ 的不透明度最大的射线为 $(0,0)(2,2)$（射线不唯一），穿过了平面镜 $2$，答案为 $10$。

对于第 $7$ 次询问，因为平面镜 $1$ 已被摧毁，所以输出 oops!。

---

数据范围与约定

测试点编号	$n\leq$	特殊性质
$1-4$	$1000$	$x,y$ 绝对值小于 $10^3$ 且没有 $4$ 询问
$5-8$	$2\times 10^5$	所有 $y$ 相等
$9-12$		$x\ge 0$
$13-20$		无

对于 $100\%$ 的数据，有 $1\leq n\leq 2\times 10^5$，$1\leq v\leq 10^3$ 且 $0\leq |x|,|y|\leq 10^5$。

保证平面镜的总数不会超过 $10^5$。

保证所有平面镜不会穿过 $(0,0)$，但不保证平面镜会退化成一个点。

保证所有 $3$ 询问 $(x,y)\neq(0,0)$。

---

对于所有测试点，时间限制 $2\mathrm{s}$，空间限制 $128\mathrm{MB}$。