题目背景

GZOI2017 D2T3

题目描述

某校校内有 A 公司与 B 公司两家共享单车公司相互竞争。A 公司为了尽可能提升自己在校园内的占有率，会设法阻碍 B 公司的回收行动。

整个校园由 $N$ 个区域和 $M$ 条道路组成，每条道路连接两个区域。校园有一个区域 $K$ 是 B 公司的大本营，所有的单车回收行动从该区域 出发。B 公司为了减少成本，回收时从区域 $K$ 到任何一个区域 $X$ 都选择长度 最短 的路径，如果有多条到某一个区域的最短路径，则选择所有最短路径中该区域的前一区域 编号最小 的一条路径，称这条路径为 $K$ 到 $X$ 的 回收路线。所有的 回收路线 组成一棵树状结构，称之为 回收路线树。如下图中，绿色的边构成的就是一棵 回收路线树。

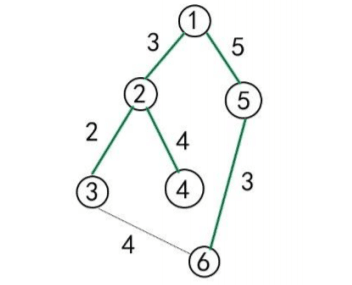
B 公司每次会回收若干个区域的单车，称这些区域为 回收区域。B 公司还将某些区域设为 投放区域，称其余区域为 非投放区域。在 回收路线树 上，标记出区域 $K$，标记出所有的 回收区域，以及标记出任意两个 回收区域 在 回收路线树 上的最近公共祖先。

如下图，假设 $4$ 与 $6$ 号区域是 投放区域，$4, 5, 6$ 号区域是回收区域，则被标记的区域有 $1, 4, 5, 6$。

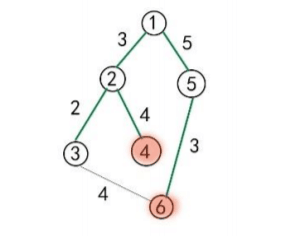
A 公司对 B 公司的回收行动造成了阻碍，当且仅当 对任意一个 $K$ 以外的被标记的 投放区域 $X$，从区域 $K$ 到 $X$ 的 回收路线上 都存在两个被标记的区域，它们之间 所有道路（回收路线树上两点路径）被阻碍。

阻碍一条道路的代价为该道路的长度。上图中 A 公司选择阻碍 $1 \rightsquigarrow 4$，$5 \rightsquigarrow 6$ 两条路径，代价为 $3+4+3=10$。

你的任务是帮助 A 公司计算如何以最小的代价，阻碍 B 公司的回收行动。

输入格式

第一行四个整数 $N, M, K, Q$ 分别表示 X 校校园内区域数量、道路数量以及 B 公司大本营的编号 $K$ 和操作数量。

第二到第 $M + 1$ 行描述道路，每行三个整数 $S,T,Len$ 表示有一条从 $S$ 出发 $T$ 结束的长度为 $Len$ 双向道路。

接下来第 $M + 2$ 行到第 $M + Q + 1$ 行，每行第一个整数表示操作类型，$0$ 表示 B 公司会改变投放区域，$1$ 表示 B 公司的一次回收行动。

操作类型为 $0$时，后接一个整数 $num$，表示 B 公司改变的区域数目，紧接着 $num$ 个数字分别表示区域编号。对于一个被改变的区域，如果它是 投放区域，把它改为 非投放区域；如果它是 非投放区域，把它改为 投放区域；

操作类型为 $1$ 时，后接一个整数 $num$ 表示 回收区域 数目，紧接着 $num$ 个整数表示 B 公司的 回收区域 编号。每次需要在 回收路线树 上重新标记。

输出格式

对于每一次回收行动，输出一行表示 A 公司对 B 公司造成阻碍的最小代价。注意，如果没有被标记的 投放区域，输出 $-1$。

6 6 1 4
1 2 3
2 3 2
2 4 4
3 6 4
1 5 5
5 6 3
0 3 3 4 6
1 3 4 5 6
0 1 3
1 4 3 4 5 6

10
6

12 11 4 5
4 1 32
4 6 42
1 3 29
7 1 17
7 10 23
9 7 21
5 6 16
2 6 28
5 8 14
8 11 11
8 12 17
1 11 1 2 3 5 6 7 8 9 10 11 12
0 4 3 11 5 2
1 4 10 9 6 11
0 4 7 8 12 11
1 4 11 2 9 10

-1
41
77

提示

【数据约束】

对于 $30\%$ 的数据，$N\le 200$，$Q\le 200$；

对于 $60\%$ 的数据，保证每次 回收区域 数量恒为 $N-1$；

对于 $80\%$ 的数据，$N\le 20000$，$M=N-1$，$Q\le 1000$，$num\le 200$；

对于 $100\%$ 的数据，$N\le 50000$，$M\le 100000$，$Q\le 1500$，$num\le 500$。

所有数据保证道路无自环，所有道路长度小于 $2000$，且区域 $K$ 任意时刻均非投放区域。