Description
给定 n 个数 a1,⋯,an。
对于一组配对 (x,y),若对于所有的 i=1,2,⋯,n,满足 ∣ax−ay∣≤∣ax−ai∣(i=x),则称 (x,y) 为一组好的配对(∣x∣ 表示 x 的绝对值)。
给出若干询问,每次询问区间 [l,r] 中含有多少组好的配对。
即,取 x,y(l≤x,y≤r 且 x=y),问有多少组 (x,y) 是好的配对。
第一行两个正整数 n,m。
第二行 n 个数 a1,⋯,an。
接下来 m 行,每行给出两个数 l,r。
Ansi 表示第 i 次询问的答案,输出 i=1∑mAnsi×i 即可。
3 2
2 1 3
1 2
1 3
10
Hint
【样例解释】
第一次询问好的配对有:(1,2)(2,1);
第二次询问好的配对有:(1,2)(2,1),(1,3)(3,1);
答案 =2×1+4×2=10。
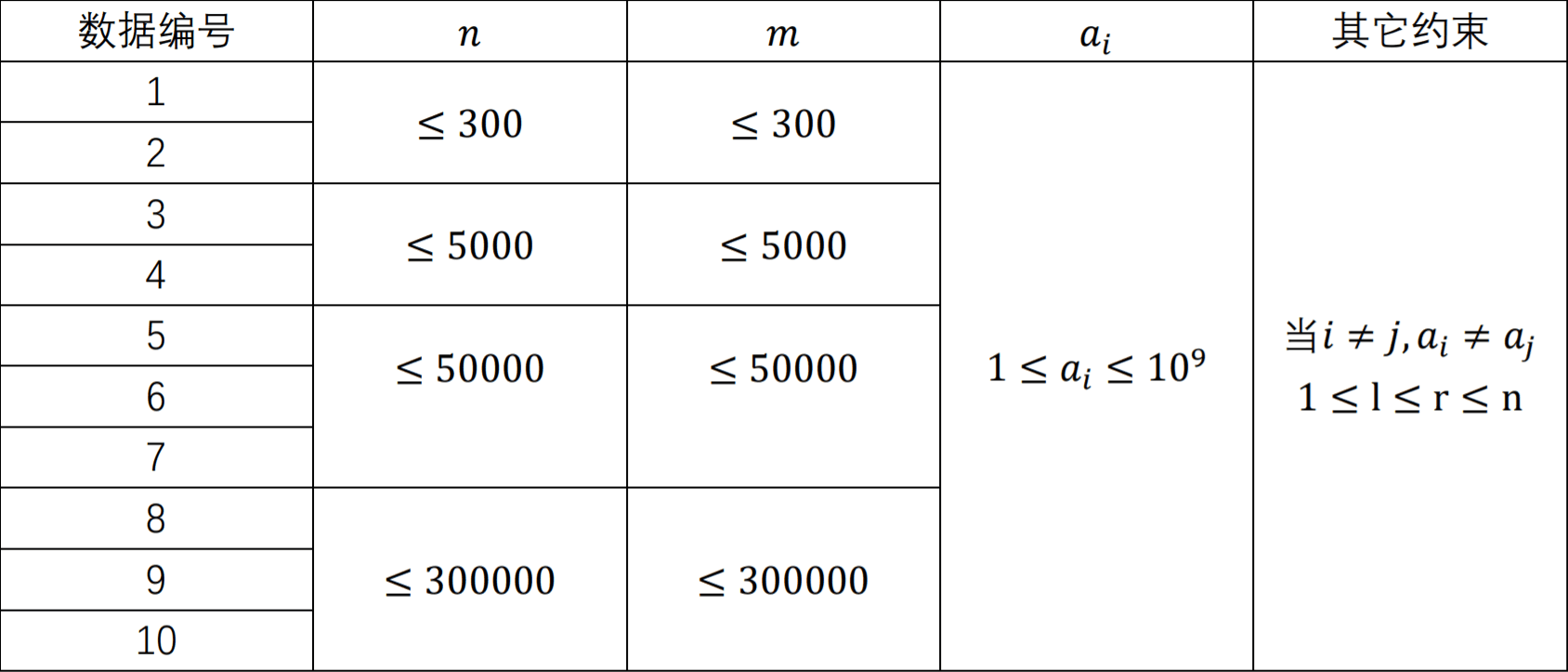
【数据约束】


 京公网安备 11011102002149号
京公网安备 11011102002149号