#P5671. 「SWTR-2」Triangles
「SWTR-2」Triangles
Description
他遇到了两个谜题:
-
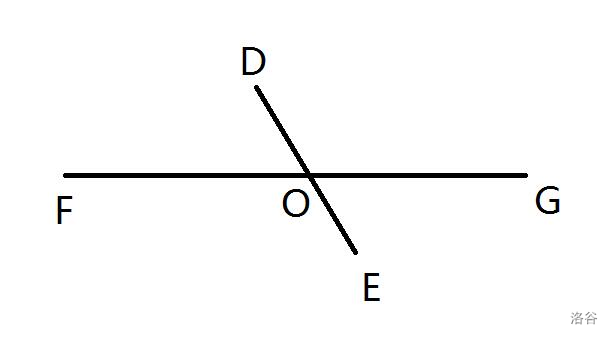
在一个平面内,线段 与直线 相交于点 ,已知 ,请你在直线 上找一点 ,使得 为等腰三角形,求 的度数。(如果答案不是整数,则保留 位小数)
-
已知一个直角三角形的两条边分别为 ,求第三条边的长度(保留 位小数)。
写一个程序求出问题的答案。
Input Format
一行三个正整数,分别为 。
Output Format
输出两行,第一行为第一问的答案,第二行为第二问的答案。
如果有多解,请用空格隔开,且从小到大输出。
60 1 1
30 60
1.41421
Hint
样例说明
问题 :
-
当点 在点 左边时,形成的 为等边三角形,。
-
当点 在点 右边时,形成的 中,,为顶角,。
问题 :
第三条边为斜边,长度为 。
数据范围与约定
。
出题组提示:
方法千万条,审题第一条,多解不考虑,爆零两行泪。

 京公网安备 11011102002149号
京公网安备 11011102002149号